Cséffai Péter[1] - Almási Bálint[2] - Dr. Bárczi Judit[3]: Közvetlen versenytársi összehasonlítás a csődelőrejelzésben (JURA, 2019/1., 219-233. o.)
I. Bevezetés
A piacgazdasági működés törvényszerűségei közé tartozik a vállalkozások keletkezése és megszűnése. Minthogy a vállalkozások megszűnése jelentős gazdasági és társadalmi kihatással is bír, így ezen események kiváltó okainak elemzése és amennyiben lehetséges úgy a bekövetkezésük előrejelzése rendkívül fontos feladat.
A csődhöz vezető folyamatok pénzügyi mutatókban kifejezhető jelzéseit az egyes kutatók már az 1930-as évektől kezdve vizsgálják. A XX. szászad második felében bekövetkezett informatikai és számítástechnikai fejlődés a csőd-előrejelzést is forradalmasította. Ennek hatására sorra jelentek meg a különböző új előrejelzési eljárások, a 60-as 70-es években a diszkriminancia-analízis, a 80-as években a logisztikus regresszió és a rekurzív partícionáló algoritmus (döntési fa), a 90-es években pedig a neurális háló.
A tanulmány egy speciális, közvetlen versenytársi összehasonlításon alapuló eljárással kíván arra a kérdésre válaszolni, hogy a vállalatok éves beszámolóiból képzett pénzügyi mutatószámok alapján mennyire biztosan jelezhető előre a csődesemény bekövetkezése. A kitűzött célok közt szerepel annak megállapítása, hogy mely tényezők játszhatnak kiemelt szerepet az előrejelzés során, illetve mely tényezők alapján különíthetők el legjobban a működő és a csődös vállalatok.
A vizsgálatok elvégzéséhez szükséges adatbázis egy saját gyűjtésű vállalati mintán alapul, melyben összesen 336 vállalat éves beszámolóinak adatai találhatók meg a 2010-2012-es időszakból. Az adatbázis felépítése során hármas csoportok kerültek létrehozásra, melyben rendre egy csődös, illetve két működő vállalat található. Az előrejelzési modellek kialakítása elsősorban statisztikai-adatelemzési eszközök felhasználásával történt. A csődös és működő vállalatok gazdasági állapotát jellemző komplex közgazdasági fogalmak elemzése, számszerűsítése érdekében a megképzett pénzügyi mutatószámok egy faktoranalitikus adattömörítő eljáráson is keresztülestek. A modellépítés a logisztikus regresszió és a többrétegű neurális háló (MLP) segítségével történt. Az egyes modellek egy-, illetve kétéves előrejelzési teljesítménye az összes helyes besorolások aránya, illetve a ROC görbe alatti terület nagysága alapján került kiértékelésre.
Az elvégzett vizsgálatok alapján a legfontosabb csőd-előrejelzési tényezők közt említhetjük a jövedelmezőséget, a tőkeszerkezetet, illetve a likviditási helyzetet. A legfontosabbnak bizonyult mutatószámok: nettó forgótőke aránya, szállítók aránya, ROA, árbevétel-arányos üzemi (üzleti) eredmény.
A kapott eredmények többségében alátámasztják az eddigi empirikus tapasztalatokat, miszerint a logisztikus regressziós eljárás és a neurális háló igen magas arányban sorolja be helyesen az egyes vállalatokat a csődös, illetve a működő kategóriákba. Az előrejelzés időtávjának növelése nagymértékben rontotta a logisztikus regressziós modellek teljesítményét. Ezzel szemben a neurális háló rugalmasabbnak bizonyult, a kétéves időtávon szignifikánsan jobban teljesített.
A speciális, közvetlen versenytársi összehasonlításon alapuló eljárással készített előrejelzések pontossága és megbízhatósága mind a két modellezési eljárás esetében jelentős javulást eredményez függetlenül attól, hogy az alap- vagy a faktorváltozók kerültek felhasználásra, illetve egy- vagy kétéves időtávra
- 219/220 -
szólnak. Az összehasonlításon alapuló eljárás további előnye, hogy alkalmazásával kiszűrhetők a szektorális és a vállalati méretből adódó torzító hatások, ezáltal általános érvényű következtetések levonására ad lehetőséget a csődfolyamatok előrejelezhetőségére és a kiváltó okok megértésére vonatkozóan.
A közvetlen versenytársi összehasonlításon alapuló adat-transzformációs eljárás a vizsgálatok alapján elérte a célját, a felhasználásával felépített modellek csőd-előrejelzésre alkalmasak, sőt minden vizsgált szempont tekintetében felülmúlják a transzformáción át nem esett, klasszikus mutatószámok értékeiből képzett előrejelzési modellek teljesítményét. Ebből kifolyólag a közvetlen versenytársi összehasonlításon alapuló adat-transzformációs eljárás ("távolság" modell) meggyőződésünk szerint további kutatások kiindulási alapját képezheti, illetve gyakorlatban történő felhasználásának tesztelése folyamatban van.
II. Szakirodalmi áttekintés
1. A csőd-előrejelzés kezdetei
A csőd-előrejelzés, mint a vállalati pénzügyek egyik kiemelt témaköre az 1960-as évek végén került a kutatások középpontjába, ekkortól kezdett dinamikusan fejlődni ez a tudományág. Az első csőd-előrejelzési modellek, illetve tanulmányok azonban már az 1930-as években megjelentek.[1] Ezek a tanulmányok első sorban egy-egy pénzügyi mutatószám kiemelt vizsgálatát tartalmazták. Az alapelv az volt, hogy a vizsgálat alapját képező mintát csődös és működő vállalatokra osztották és ezek pénzügyi mutatószámait hasonlították össze.[2] Ugyan nem tartoznak a legmegbízhatóbb és legpontosabb csőd-előrejelzési eljárások közé, mégis a mai napig felhasználják az egytényezős elemzéseket és hosszú távon még mindig használhatónak bizonyulnak.[3]
2. A diszkriminancia-analízis térhódítása
Altman 1968-ban megalkotta máig meghatározó, többváltozós diszkriminancia-analízisen alapuló Z-modelljét, melyben 66 közepes méretű ipari vállalatot hasonlított össze. Ezzel a modellel Altman 95%-os pontossággal tudta besorolni mintája vállalatait egy évre előre.[4] Fontos megjegyezni, hogy amikor egy tesztelő (hold-out) mintán is kipróbálták a modellt a helyes besorolások aránya 79%-ra esett vissza.[5] A Z-modell alapjában véve azonban csak a tőzsdére bevezetett ipari cégeken volt alkalmazható. Bár Kecskés és Halász szerint a tőzsdei árfolyamok fontos mutatószámként funkcionálhatnak[6] egy vállalat működése során, azonban nem szabad megfeledkezni arról, hogy számos vállalat nem a tőzsdéken működik. Altman és Lorris egy későbbi tanulmányukban orvosolják ezt a hiányosságot, így modelljük nem tőzsdei (OTC) vállalatoknál is alkalmazhatóvá vált.[7] A modell következő lényegesebb átdolgozására 1977-ben került sor. Az új, ZETA modellt Altman két szerzőtársával Haldemannal és Narayannal készítette el.[8] A ZETA modell hosszabb (5 éves) időtávra vonatkozó előrejelzéseivel jelentősen meghaladta a klasszikus Z-modell előrejelzési képességét. Zéman és Béhm külön felhívják a figyelmet arra, hogy a kidolgozott matematikai, statisztikai csődelőrejelzési modellek mennyiben képesek hozzájárulni a szervezetek fennmaradásával és csődbejutásával foglalkozó gazdaságelméleti megfontolásokhoz.[9]
3. A regressziós eljárások
A logisztikus regressziós eljárás (logit) és közeli rokona a probit analízis feltételes valószínűségen alapuló modellek.
Az első logisztikus regresszión alapuló modellt James A. Ohlson publikálta 1980-ban. Ohlson egy 2163 iparvállalatból álló mintából építette fel új modelljét. A modellben 105 csődös vállalat szerepelt. Ezzel Ohlson azt is figyelembe vette, hogy a csődbe ment vállalatok aránya az összes vállalaton belül sokkal kisebb, így ezzel a modellel általános következtetések is levonhatók voltak. Ohlson a reprezentatívnak tekinthető mintán összesen 82,9%-os helyes besorolási arányt ért el, 12,4%-os elsőfajú és 17,4%-os másodfajú hibaarány mellett.[10] Az eljárás annyira forradalmi volt, hogy a 80-as évek meghatározó csőd-előrejelzési módszere lett, illetve a 90-es évek közepéig a leggyakrabban használt eljárás volt.
- 220/221 -
A regressziós modellek másik nagy csoportját a probit analízist használó modellek alkotják. A probit analízis csőd-előrejelzésben való felhasználása Mark E. Zmijewski 1984-es tanulmánya után kezdett el fejlődni. A későbbiek során azonban nem terjedt el annyira, mint az ohlsoni logit analízis, mivel alkalmazása nehézkesebb.
4. Rekurzív partícionáló algoritmus (RPA, döntési fa)
Az RPA-k már nem a klasszikus, parametrikus statisztikai módszerek közé sorolhatók be, hanem a szimulációs eljárások családjához tartoznak. Az RPA-t csőd-előrejelzésre először a H. Frydman - E. I. Altman - D. Kao szerző trió alkalmazta 1985-ben. Ebben a tanulmányukban nem csak egy új klasszifikációs eljárást mutattak be, hanem össze is hasonlították az eljárás teljesítményét a diszkriminancia-analízis alapú modellével. A felépített modell az összes vállalat 94%-át sorolta be helyesen, továbbá a működő vállalatokat 99%-ban.[11]
5. A mesterséges intelligencia alapú neurális háló modellek
A neurális hálót csőd-előrejelzésre először Odom és Sharda alkalmazta, melynek eredményeit 1990-ben hozták nyilvánosságra tanulmányukban. Odom és Sharda felülvizsgálta Altman 1968-as tanulmányát, pontosabban az ott alkalmazott öt mutatószámot használta fel a modell építése során, melyet egy 74 vállalatból álló mintán teszteltek és ennek eredményeit összevetették a diszkriminancia-analízisével.
A kapott eredmények megdöbbentőek voltak. A neurális háló nagymértékben felülmúlta a diszkriminancia analízist, és tökéletes besorolást is elértek. Vagyis minden egyes vállalatot helyesen soroltak be. Egy tesztelési (hold-out) mintán is lefuttatták a neurális háló modellt, ahol az szintén felülmúlta a diszkriminancia analízist, ugyanis a modell számára ismeretlen mintán 82%-os pontossággal azonosította a csődös vállalatokat, míg a diszkriminancia-analízis csak 60%-os teljesítményt nyújtott.[12]
Egy másik megjelenési formáját a mesterséges intelligencia alapú neurális hálóknak a csőd-előrejelzésben az önszerveződő térképek jelentik (Self Organizing Map, SOM). Az önszerveződő térképek specialitása, hogy nincsenek megadva előre azok a csoportok (csődös, működő), amikbe be kell kategorizálni az egyes vállalatokat a mutatószámaik alapján. Ebben a formában a neurális hálót egyfajta klaszterezési eljárásnak tekinthetjük.
"A felülvizsgálatlanul tanuló neurális hálók elvén működő önszerveződő térképeket először Kiviluoto alkalmazta csődelőrejelzésre különböző időhorizontokon finnországi vállalatok beszámolóira építve. A vizualizációs technikákat felvonultató önszerveződő térképek minden idők leglátványosabb eredményét produkálták."[13]
A módszer előnyei közé tartozik, hogy a térképszerű megjelenítést felhasználva felfedezhetünk olyan területeket, ahol nagyobb a csőd kockázata, illetve figyelemmel kísérhetjük egy vállalat állapotának időbeli változását, térképen való elmozdulását. Az eljárás hátránya ugyanakkor, hogy a változók előszelekciójára van szükség.[14]
III. A felhasznált minta és módszerek bemutatása
1. A minta bemutatása
A kutatás kezdetekor nem állt rendelkezésre egy előre felépített adatbázis, így a nyilvánosan elérhető pénzügyi beszámolók, céginformációk kerültek felhasználásra. A minta felépítéséhez alkalmazott eljárás során először létrehozásra került egy lista a csődbe ment vállalatokról. A következő lépésben a működő vállalatok hozzápárosításra kerültek (egy csődöshöz két működő) a csődös vállalatokhoz, hasonlóan a Mures-Quintana - Garcia-Gallego szerzőpáros által alkalmazott eljáráshoz.[15] Az eljárás előnye, hogy így több csődös vállalathoz jutunk, hiszen a normálisan működő gazdaságban a csődös vállalatok aránya csekélynek mondható (Zmijewski [1984]). Hátránya ugyanakkor a véletlenszerűség hiánya.[16]
Mivel a szakirodalomban nincs egységes állásfoglalás a csődesemény definícióját és kezdő időpontját tekintve, ezért a csődös mintát olyan vállalatok képezik, melyek csőd-, illetve
- 221/222 -
felszámolási eljárás alá kerültek a 2011-2013-as időszakban. A minta összesen 336 vállalat - 112 csődös és 224 működő - pénzügyi beszámolóiból áll, a 2009-2012-es időszakból.
A vállalatok összehasonlíthatóságának biztosítása (működési területi, méretbeli, nagyságrendi, időbeli), illetve a beszámolókból nyerhető információk mennyisége, minősége és értelmezhetősége érdekében a minta felépítése során egy többlépcsős szűrőrendszer került kialakításra.
A mintába kerülés szűrőfeltételei:
- az adott cég éves beszámolót készítsen,
- erre leginkább az adott vállalatok mérete miatt volt szükség, hiszen így a kis- és középvállalatok közül csak a nagyobbak kerülhettek a mintába, a mikro vállalkozások kizárásra kerültek;
- legalább három teljes üzleti évet lezáró beszámoló elkészítése
- az evolúciós szervezetelmélet empirikus alátámasztásai kimutatták, hogy az új szervezetek nagyobb valószínűséggel szűnnek meg, mint a régebb óta fennálló szervezetek;[17]
- a csődöt megelőző két üzleti év valamelyikében legalább 500 Mft-os árbevétel,
- sok vállalat ugyan éves beszámolót készített, azonban az árbevétel nagysága alapján arra lehetett következtetni, hogy legalább 3-4 éve nem folyik üzletszerű tevékenység, illetve annak volumene túlságosan csekély ahhoz, hogy ne torzítsa a későbbi elemzések eredményét[18];
- a csődöt megelőző két üzleti év valamelyikében legalább 300 Mft-os mérlegfőösszeg,
- ez, mint utólag kiderült egy puha korlátnak bizonyult, de a cél az volt, hogy azért számottevő vagyon legyen az adott vállalakozás irányítása alatt;
- az adott vállalat éves beszámolója ne tartalmazzon kirívó, javíthatatlan hibákat,
- sok vállalatnál elképzelhetetlen hibák is feltárásra kerültek, melyeket még az előző és rá következő évben is szerepeltettek. Ilyen volt többek között a negatív értékhelyesbítés esete, illetve, ha eszköz oldalon volt értékhelyesbítés, viszont forrás oldalon nem volt értékelési tartalék. Ugyan ezzel még nem lehet alátámasztani, hogy az adott beszámoló nem felel meg a számviteli törvény előírásainak, ám mivel a beszámolók túlnyomó része könyvvizsgálattal alátámasztott volt, így elegendőnek tekinthetjük csak a kirívóan hibás beszámolók kizárását.[19];
- amennyiben anyavállalat kerülne a mintába, úgy legyen elérhető a konszolidált beszámoló is, hiszen végül annak az adatai kerülnek be a mintába;
- működő vállalat esetén fontos, hogy nagyságrendileg[20] megegyezzen a csődös "párjával", legyen éves beszámolója a megfelelő időszakból, illetve azonos szakágazatban tevékenykedjen.
Az mintagyűjtés következő lépésében megtörtént a beszámolók szerkezeti egységesítése és az egy adatbázisba történő felvétel. A mintából elhagyásra kerültek az építőipari (TEÁOR: 41-43), a vendéglátással foglalkozó (TEÁOR: 55-56), a pénzügyi szolgáltató (TEÁOR: 64-66), az ingatlan adás-vétellel foglalkozó (TEÁOR: 68) cégek. A pénzügyi szolgáltatók, hitelintézetek kizárására azért volt szükség, mivel beszámolójuk lényeges eltérést mutat és működésük is teljesen speciális szabályoknak kell, hogy megfeleljen. Az áttekintett építőipari, vendéglátó és ingatlanforgalmazó cégek beszámolóinak elhagyására pedig azért volt szükség, mivel azok adatainak minősége nagymértékben torzította volna a további elemzéseket.
2. A megképzett pénzügyi mutatószámok
Az elemzések elvégzéséhez eredetileg mintegy 110 pénzügyi mutatószám került meghatározásra. A sok mutató megképzésének célja, hogy a lehető legpontosabban lehessen felmérni az adott vállalkozás vagyoni, pénzügyi és jövedelmezőségi helyzetét. A megképzett mutatók ezután egy elsődleges szűrésen estek át. Kiszűrésre kerültek azon mutatók, melyek potenciálisan fals eredményt mutathatnak (pl. ROE); a vállalatok több, mint 10%-ában nem voltak számíthatók; nem bruttó cash flow ala-
- 222/223 -
pú mutatók (pl. cash-flow arányos jövedelmezőség).
További előkészítő lépések voltak szükségesek az adatbázis minőségének, a mutatószámok matematikai összehasonlíthatóságának biztosítása érdekében és az egyes előrejelzési modellek érzékenysége miatt. Ezek közé tartozott a kiugró értékek kezelése, a hiányzó adatok pótlása és a változók standardizálása (közös mércére helyezése).
A kiugró, extrém adatok az ún. 3 szigma szabály szerint trimmelésre kerültek, ami azt jelenti, hogy ezeket a kiugró adatokat az adott változó szórásának ±3-szorosával helyettesítjük. Ezzel megnyírva, trimmelve az adott változó értékeit.
Alkalmazásra került az az adatbányászatban elfogadott eljárás, hogy a hiányzó értékeket (amennyiben azok számossága nem haladja meg a minta 10%-át) az adott változó átlagával helyettesítjük.
A változók standardizálására azért volt szükség, mert az egyes pénzügyi mutatószámok más és más mértékegységben voltak, ebből adódóan az értékkészletük intervallumát tekintve meglehetősen nagy eltérések voltak tapasztalhatók, amik az egyes modellezési eljárásoknál (faktoranalízis, logisztikus regresszió) torzításként jelentkeztek volna.
3. A közvetlen versenytársi összehasonlításon alapuló speciális eljárás (a "távolság" modell)
A minta egyedi felépítéséből adódóan vállalkozási triókat lehet létrehozni, melyekre jellemző, hogy egymás versenytársai a működő piacokon. A triókra igaz, hogy ugyanabban a szakágazatban tevékenykednek, a tevékenységük volumene (árbevétel) és az általuk irányított vagyon (mérlegfőösszeg) mérete azonos nagyságrendű, továbbá, hogy nem tartoznak a fiatal (3 évesnél fiatalabb) vállalatok közé.
A minta egyedi felépítésének előnyei egy speciális eljárással kerültek kihasználásra, melynek lényege egy adott változónál (pénzügyi mutatószámnál), hogy különbségeket képzünk a vállalatok közt és ezeket a különbségeket átlagolva sorrendet képzünk az egyes vállalatok közt a vállalat-hármasokon belül. Vegyünk példaképp egy vállalat-hármast, melynél a csődös vállalatot jelölje CS, továbbá a két működő vállalatot M1 és M2. A ROA mutató (adózott eredmény/összes eszköz) feltételezett értékei: 10% (M1), 12% (M2), 5% (CS) (1. táblázat).
A cél, hogy az egyes vállalatok többi vállalattól mért távolságát (különbségét) átlagoljuk, így a két különbséget egy értékkel is leírhatjuk. Tehát M1-re adódik, hogy (-2+5)/2= 1,5; ehhez hasonlóan M2-re: 4,5; CS-re:-6.
Azonban ha összeadjuk a kapott értékeket természetesen nullát kapunk. Ez az elemzésekben torzításként jelentkezne, így az átlagos eltéréseket az abszolút értékükkel beszorozva M1-re adódik: M1: 1,5 * |1,5| = 2,25; M2 = 20,25; CS = -36.
A módszer előnyei közé tartozhat, hogy mivel csak a hasonló, konkurens vállalatok közti különbségeken alapul, így a többi vállalkozás-hármassal összehasonlítva kiküszöbölhetők lesznek az egyes szektorális, méretbeli hatások.
Általában a statisztikai eljárások úgy működnek, hogy a csődös és a működő vállalatok általános tulajdonságai közt keresik a különbséget, azonban ez az alternatív eljárás megfordítja ezt a gondolatmenetet és a fellelhető különbségekre alapozva keres valamilyen általános igazságot.
A kutatás során minden modellezési eljárás és a faktoranalízis is elvégzésre került mind a normál pénzügyi mutatószámokkal, mind pe-
1. táblázat: A "távolság" modell működése
| Vállalat neve | Működő 1 | Működő 2 | Csődös | Átlagos eltérés | Abszolút eltérés | Távolság érték |
| Működő 1 | 0 | 10-12= -2 | 10-5= 5 | 1,5 | 1,5 | 2,25 |
| Működő 2 | 12-10= 2 | 0 | 12-5= 7 | 4,5 | 4,5 | 20,25 |
| Csődös | 5-10= -5 | 5-12= -7 | 0 | -6 | 6 | -36 |
Forrás: saját szerkesztés
- 223/224 -
dig a közvetlen versenytársi összehasonlításon alapuló speciális adat-transzformációs eljárás által kapott "távolság" értékekkel.
4. Faktoranalízis
A faktoranalízisek és a további statisztikai elemző és modellépítő eljárások az SPSS 22.0 programmal történtek.
A különböző vállalatok gazdasági állapotának, teljesítményének mérése igen összetett feladatot jelent. A közgazdaságtanban fellelhető összetett fogalmak (jövedelmezőség, likviditás, tőkeszerkezet) leírása, számszerűsítése elengedhetetlen a csődfaktorok beazonosítása érdekében. Az egyes változók szelektálásához, illetve a komplex fogalmak számszerűsítéséhez a hazai gyakorlattól eltérően nem a főkomponens-elemzés, hanem a sok változó miatt az ún. ULS (Unweighted Least Squares) eljárás került alkalmazásra. A legkisebb négyzetek (ULS) módszerének lényeges tudnivalója, hogy "Ez a módszer minimalizálja a megfigyelt és a modell által reprodukált kovarianciák különbségét. A módszer előnye, hogy a változók eloszlása lényegtelen [...]"
A faktorképzés egy iteratív eljárás, hiszen elsőre nem biztos, hogy kellő mértékben sikerül tömöríteni a változókban foglalt információt, valamint nem minden változó jellemzi teljes egészében ugyanolyan jól az egész mintát. A faktorelemzés (és minden iteráció) előtt meg kell vizsgálni azonban, hogy a bevont változók alkalmasak-e az eljárás lefolytatására.
Akkor tekinthetjük alkalmasnak a változórendszert a faktorelemzésre, ha:
- a változók közti korrelációk nem kiugróan erősek
- amennyiben két változó közti korreláció értéke meghaladja a ±0,9-et, akkor majdnem kifejezhető az egyik a másikkal, majdnem függvényszerű a kapcsolat
- ebből kifolyólag a ±0,9-et meghaladó korrelációt felmutató változópárok közül az egyik eliminálásra került;
- az ún. anti-image kovariancia mátrix főátlón kívüli elemeinek kevesebb, mint negyede lehet 0,09-nél nagyobb;
- az ún. anti-image korrelációs mátrix főátlójában levő elemek mindegyike lehetőleg 0,5 felett van;
- a modell-megfelelőségi mérték (KMO érték) legalább 0,5;
- az összes magyarázott szórásnégyzet hányad legalább 60-80%.
Az egyes változók eliminálására kerülnek abban az esetben, ha:
- az anti-image korrelációs mátrix főátlójában kisebb, mint 0,5-es értéket vesz fel;
- a kommunalitás értéke 0,5 alatt van.
A faktor elemzés végső lépése, a tömörítés matematikai megfogalmazása. Ez egy regressziós eljárás keretében történik. Egy adott vállalat adott faktorra vonatkozó pontszámát úgy kapjuk, hogy a faktorelemzésbe bevont változókat szorozva összegezzük az ún. rotált faktor-koefficiensekkel.
5. Logisztikus regressziós modellek
A logisztikus regresszió annyiban hasonlít a diszkriminancia-analízishez, hogy ez az eljárás is egy függvényt hoz létre, amibe az adott vállalat mutatószámait kell behelyettesíteni. A különbség az, hogy a logisztikus regresszió az előre definiált csoportba (csődös, működő) tartozás valószínűségét adja meg. Ha az előre megadott (cél)csoportba tartozás valószínűsége meghalad egy bizonyos értéket (általában a 0,5-öt), úgy a vállalat a besorolásra kerül a (cél)csoportba. Ezt a bizonyos értéket, ahol a "vágás" történik nevezik cut-off value-nak. A cut-off value értékének meghatározása az előrejelzési célok függvényében változhat. Előrejelzési cél lehet például a lehető legtöbb működő vagy legtöbb csődös vállalat megtalálása, illetve összesítve a legtöbb helyes besorolás elérése. Az logisztikus regresszió által létrehozott valószínűségi értékek és a cut-off value megváltoztatása az eljárás felhasználhatóságát is megkönnyíti, hiszen kockázatkezelési szempontból a valószínűségeket könnyebb alkalmazni, mint az altmani Z értékeket. Az eljárás előnye, hogy viszonylag kevés megkötést igényel és kiváló eszköz a magyarázó változók és egy bináris változó közti kapcsolat leírására. Hátránya ugyanakkor, hogy a modellépítéshez felhasznált változók kiugró értékeire igen érzékeny.
- 224/225 -
A logisztikus regressziós modell matematikai alakja
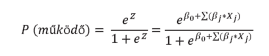
ahol
ßj regressziós paraméter
Xj a magyarázó változók (pénzügyi mutatószámok)
j=1,...m, ahol m a pénzügyi mutatók száma
A logisztikus regresszió alapú modell elkészítéséhez a forward: LR módszer került alkalmazásra. A módszer lényege, hogy minden lépésben egy új változót von be, a beléptetési kritériumok a Wald-féle beléptetési kritériumok voltak 5%-os és 10%-os szignifikancia szinten.
6. Neurális háló alapú modellek
A neurális hálók lényegében megpróbálják leutánozni a biológiai idegrendszerek információ-felvételének és feldolgozásának a folyamatát, tehát nem algoritmikus eljárásokkal, hanem tanulás útján lesznek képesek arra, hogy bizonyos feladatokat el tudjanak végezni. (1. ábra)
A neurális hálók alapját az elemi neuronok adják. A neuron egy olyan több-bemenetű, egy-kimenetelű eszköz, mely az inputokat valamilyen választott nemlineáris leképzéssel outputokká alakítja.[21] (2. ábra)
A csőd-előrejelzés során az input réteg neuronjai tartalmazzák az egyes megadott változókat. Az input neuronok kapcsolatban vannak a köztes réteggel, a kapcsolatok fontosságuk szerint súlyozva vannak és a tanulás lényege, hogy a köztes réteg súlyai folyamatosan változnak a tanulási időszak alatt. Ugyanez a folyamat játszódik le eggyel magasabb szinten, ahol a köztes réteg neuronjai kapcsolódnak az output neuronhoz (aminek két kimenete: csődös, működő), majd a folyamat eredményeképp kialakításra kerül a háló végleges súlyozása, a tanulási folyamat lezárul. Amikor egy neurális hálót először töltünk fel adatokkal, akkor először véletlenszerűen fogja az egyes súlyokat meghatározni, majd megvizsgálja, hogy az így elért eredmény mennyire tér el a tényleges eredménytől és ennek alapján módosítani fogja az egyes neuronok közti súlyokat.[22] (3. ábra)
A tanulási folyamat során folyamatosan figyelni kell a túltanulásra utaló jelekre. A túltanulás az a jelenség, amikor a háló a tanuló minta sajátosságaira specializálódik, nem az általános problémát tanulja meg kezelni (gyakorlatilag "bemagolja" a tanulási mintát). Ennek jele, hogy a háló megedzésére szolgáló tanuló mintán jóval pontosabb besorolást érünk el, mint az ismeretlen tesztelő mintán.
A neurális hálók létrehozása minden esetben a többrétegű neurális háló (MLP, Multi-Layer
1. ábra: A neuron működése
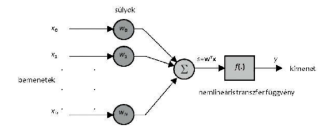
Forrás: Altrichter, et. al. [2006]
2. ábra: Egy háromrétegű neurális háló felépítése

Forrás: Kovács im.
3. ábra: A neurális hálók tanulása a backpropagation eljárással

Forrás: Kristóf [2008a] p. 64
- 225/226 -
2. táblázat: A létrehozott neurális hálók tulajdonságai
| A neurális háló alapadatai | Bevont változók száma | A neurális háló felépítése |
| Alapváltozók, "normál" értékek | 30 | 30-8-3-2 |
| Faktorváltozók, "normál" értékek | 6 | 6-3-2 |
| Alapváltozók, "távolság" értékek | 23 | 23-8-2 |
| Faktorváltozók, "távolság" értékek | 6 | 6-4-3-2 |
Forrás: saját szerkesztés
Perceptron) eljárással és a backpropagation tanulási algoritmussal készült. (2. táblázat)
7. A modellek teljesítményének értékelése
A modellek teljesítményének mérésére a szakirodalomban két leginkább elterjedt eljárás alapján került sor. Az egyik a klasszifikációs mátrix és az abból eredeztethető hibaarányok, míg a másik az ún. ROC görbe és a görbe alatti terület nagysága.
Klasszifikációs mátrix
Időben először a klasszifikációs mátrix jelent meg, amit a 3. táblázat szemléltet.
A besorolás, előrejelzés szempontjából elsőfajú hibának tekinthető, ha a valóságban működő, túlélő vállalatot csődösnek soroljuk be. A másodfajú hiba ennek megfelelően azt jelenti, hogy a valóságban csődös vállalatot működőnek tituláljuk.
Az előrejelzés és annak gyakorlati alkalmazása során világos, hogy a másodfajú hiba elkövetésének nagyobb költségei lehetnek Például, ha egy bank egy csődveszélyben levő vállalatot fizetőképesnek minősít és hitelt nyújt neki, úgy nem csak a kamatot, de a kihelyezett kölcsönt is elbukhatja. Fordított esetben egy működő, túlélő vállalattól tagad meg egy hitelt, ami legfeljebb a kamatbevételek elmaradását eredményezheti.
A táblázatból több mutatószám is származtatható, ám leginkább az ún. sensitivity és specificity mutatószámok használata vált elterjedté.

A ROC (Receiver Operating Characteristic) görbe
A ROC görbe lényegében a fenti két mutatószám alapján elkészített grafikon. Nagy előnye, hogy grafikusan szemlélteti a kapott eredményeket. A két dimenziója:
- "x" tengelyen találhatók a 1- SPECIFITY értékek, amik gyakorlatilag a téves negatív riasztások arányát jelentik;
- "y" tengelyen pedig a SENSITIVITY értékek, amik a helyes pozitív besorolások arányát jelentik;
- a görbe specialitása, hogy minden egyes lehetséges cut-off ponton átmegy, így segítségével leolvasható lesz a helyes pozitív és fals pozitív (téves riasztások) aránya;
- a görbe alapján minden egyes cut-off pontra becsülhető az első- és másodfajú hibák nagysága.
Az értékeléshez hozzátartozik, hogy a teljesen véletlenszerű besorolást jelentő görbe egyenle-
3. táblázat: A klasszifikációs mátrix felépítése
| Valóság | |||
| Csődös | Működő | ||
| Előrejelzés | Csődös | True positive (TP) helyes csődös besorolás | False positive (FP) elsőfajú hiba |
| Működő | False negative (FN) másodfajú hiba | True negative (TN) helyes működő beso- rolás | |
| Sensitivity | Specificity | ||
Forrás: saját szerkesztés Jánosa [2011] alapján
- 226/227 -
te y=x lesz, míg a tökéletesen osztályozó besorolás görbéjének át kell mennie a (0:1) ponton. A modell teljesítményének mérésére a görbe alatti terület kiszámítása (Area Under the ROC, AUROC). Az AUROC értéke 0,5 és 1 közé esik (százalékos kifejezése is elfogadható) és minél közelebb van az 1-hez (100%) annál jobbnak tekinthető a teljesítménye. (4. ábra)
IV. Az elvégzett vizsgálatok eredményei
1. Faktorelemzés
Az elvégzett faktorelemzések eredményeit a 4. táblázat foglalja össze.
Látható, hogy mind a "normál", mind a "távolság" értékeken megképzett faktorok magas modell-megfelelőségi (KMO) értékkel rendelkeznek, valamint az adattömörítés sikerességét mutató TVE %-ok is elfogadhatónak tekinthetők.
A létrejött faktorok további felhasználásához nélkülözhetetlen azok lineáris függetlensége, melynek ellenőrzése korreláció-elemzéssel történt és a lineáris függetlenség a kapott eredmények alapján fennáll.
Az egyes faktorok és faktorértékek csőd-előrejelzés szempontjából kedvező irányának meghatározása:
1) Jövedelmezőség: a nagyobb faktor érték kedvezőbb jövedelmezőségi helyzetet mutat;
4. ábra: A ROC görbe felépítése
a) az elsőfajú hiba nagysága; b) a másodfajú hiba nagysága; AUROC) a görbe alatti terület
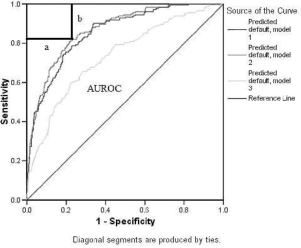
Forrás: saját szerkesztés
2) Eszközgazdálkodás: a faktort alkotó változók nagyságának megítélése vegyes képet mutat, azonban t-tesztek alapján kijelenthetjük, hogy a csődös vállalatok jellemzően alacsonyabb forgóeszköz-aránnyal és rosszabb eszköz-fedezettséggel rendelkeznek, valamint alacsonyabb követelés-arányuk sem biztos, hogy a jól működő követelés kezelő rendszerek miatt alacsonyabb, feltehetőleg a tevékenység volumenének csökkenése miatt; ezekből kifolyólag a nagyobb faktor értéket tekinthetjük elvártnak a vállalati túlélés érdekében;
4. táblázat: A faktorelemzés eredményei
| "Normál" értékek | "Távolság" értékek | |
| Kezdeti változók száma | 30 | 23 |
| Faktor 1 | Jövedelmezőség | Erőforrás-arányos jövedelmezőség |
| Faktor 2 | Eszközgazdálkodás | Tőkeszerkezet |
| Faktor 3 | Azonnali fizetőképesség, likviditás | Eszközszerkezet |
| Faktor 4 | Tőkeszerkezet | Likviditás, kötelezettség-fedezet |
| Faktor 5 | Növekedés | Bevétel-arányos jövedelmezőség |
| Faktor 6 | Partner-management | Növekedés |
| KMO érték | 0.859 | 0.812 |
| TVE* | 75.22% | 73.50% |
* TVE, Total Variance Explained - A faktormodell által magyarázott összes variancia hányad
Forrás: saját szerkesztés
- 227/228 -
3) Azonnali fizetőképesség szintén a nagyobb faktor érték jelent kívánatosabb helyzetet;
4) Tőkeszerkezet: a faktor lényegében a működési biztonságot és függetlenséget mutatja a magasabb faktor érték fontos a túléléshez;
5) Növekedés: a vállalkozások tevékenységének és vagyonának növekedése mindenképp kívánatos a túléléshez, ezért ennél a faktornál is a nagyobb faktor értéket tekintjük jónak;
6) Partner management: a faktort alkotó két mutató követelés / kötelezettség alapon épül fel; a minta alapján a működő vállalatoknál nagyobb a kapott faktor érték, ami azt is jelenti, hogy a képesség, hogy a vevőiket finanszírozzák, és ne magukat finanszíroztassák a szállítóikkal fontos megkülönböztető jegye lehet a csődös és a működő vállalatoknak, éppen ezért itt is a magasabb faktor érték pozitív elbírálás alá esik.
Érdekes módon a "normál" értékek alapján megképzett faktorokkal nagy hasonlóságot mutat a "távolság" értékekkel képzett faktor-együttes. A legszembetűnőbb változás, hogy a jövedelmezőség faktor két részre szakadt (eszköz- és bevétel-arányos) és a "távolság" értékek alapján készített faktor modellben nem szerepel külön faktorként a partner management. Az egyes faktor értékek nagyságára és irányára vonatkozó értékelés megegyezik a "normál" értékekből képzett modellével.
2. A modellezési eljárások által felhasznált változók
Az alapváltozók jelen esetben a faktorizációs eljárás utolsó lépése előtti változókat jelentik, mivel az iteratív faktorizációs folyamat természetéből adódóan ezek a változók jellemzik legjobban a sokaságot. (5. táblázat)
A "normál" értékek alapján felépített modellek által felhasznált változók igen széles skálán mozognak. A logisztikus regressziós modell elsősorban a likviditási mutatókat használta fel, ez alapján azt a következtetést vonhatjuk le, hogy a likviditás tekintetében van a legnagyobb különbség a csődös és a működő vállalatok közt. Ennek ellentmond, hogy a faktorváltozókra épülő logit modell legfontosabb változója a jövedelmezőség, csak ezután következik a likviditás. A neurális háló esetében a fontossági elemzés alapján a ROS, illetve az üzemi eredmény/árbevétel mutatók a legfontosabbak. Az első két mutató a bevétel-arányos jövedelmezőségi mutatók közé tartozik. Ezután következik a szállítók aránya és a nettó forgótőke aránya, amik pedig a tőkeszerkezeti mutatókhoz tartoznak. A faktorváltozókat
5. táblázat: Az egyes modellek által felhasznált változók
| "Normál" értékek | "Távolság" értékek | ||||||
| Logisztikus regresszió | Neurális háló | Logisztikus regresszió | Neurális háló | ||||
| Alap- változók | Faktor- változók | Alap- változók | Faktor- változók | Alap- változók | Faktor- változók | Alap- változók | Faktor- változók |
| Bruttó CF/ Röv.lej.köt. | Jövedelme- zőség | ROS | Jövedelme- zőség | Nettó forgó- tőke arány | Tőkeszerke- zet | Szállítók aránya | Tőkeszerke- zet |
| Nettó forgó- tőke arány | Likviditás | Üzemi eredmény/ üzemi bevé- telek | Tőkeszerke- zet | Üzemi eredmény/ Árbevétel | Bevétel-ará- nyos jöve- delmezőség | Üzemi eredmény/ Árbevétel | Bevétel-ará- nyos jöve- delmezőség |
| Vevő/szállí- tó arány | Tőkeszerke- zet | Szállítók aránya | Partnerma- nagement | ROA | Erőfor- rás-arányos jövedelme- zőség | Nettó forgó- tőke arány | Erőfor- rás-arányos jövedelme- zőség |
| Növekedés | Forgóeszköz növekedés | Likviditás | Szállítók aránya | Likviditási, kötelezett- ség-fedezet | ROA | Likviditási, kötelezett- ség-fedezet | |
| Partnerma- nagement | Nettó forgó- tőke aránya | Növekedés | Növekedés | Bruttó CF/ Röv.lej.köt. | Növekedés | ||
Forrás: saját szerkesztés
- 228/229 -
használó neurális háló legfontosabb mutatója a jövedelmezőség faktor, ami egybe cseng az alapváltozókat használó háló eredményével.
A "távolság" értékeknél mind a két eljárás alapján ugyanazok a legfontosabb mutatók. Ebből azt a következtetést vonhatjuk le, hogy a nettó forgótőke aránya, valamint a ROA és az árbevétel arányos üzemi eredmény szempontjából a versenytársakhoz mért elmaradás nemcsak, hogy versenyhátrány, de egyenesen a vállalat jövőjét veszélyeztető tényező. A szállítók arányánál ez fordítva igaz, tehát a versenytársakhoz képest nagyobb szállító-arány jelenti a nagyobb csődveszélyt. A felhasznált faktorváltozók tekintetében az az érdekes helyzet állt elő, hogy mind a logisztikus regresszió, mind a neurális háló ugyanolyan fontossági sorrendet állapított meg az egyes faktorok csőd-előrejelző képességét tekintve. A faktorok fontossági sorrendje nagyjából megegyezik az alapváltozók sorrendjével, hiszen a nettó forgótőke aránya és a szállítók aránya tőkeszerkezeti, míg a másik két mutató jövedelmezőségi mutató.
A "normál" és a "távolság" értékeket használó modellek által bevont változókat összehasonlítva a legfontosabb csőd-előrejelző változók a nettó forgótőke aránya, a ROA, a szállítók aránya, valamint az árbevétel-arányos üzemi eredmény. Érdekes, hogy eszközszerkezeti mutatók, valamint a cash-flow alapú és pénzeszközökkel kapcsolatos mutatók nem kerültek felhasználásra. A minta alapján ez arra enged következtetni, hogy a csődös vállalatok eszközszerkezete, - gazdálkodása nem tér el szignifikánsan a működő vállalatokétól, a csődjelzéseket a forrásoldalon, a finanszírozás módjánál és a működési teljesítménynél kell keresni. Ezt a faktorváltozós modellek is alátámasztják, hiszen a tőkeszerkezet és a jövedelmezőségi faktorok igen előkelő helyen szerepelnek a fontossági sorrendben.
3. Az alapváltozókat felhasználó modellek teljesítmények értékelése
A modellek felépítéséhez véletlenszerűen kiválasztásra került egy tanulási minta (75%), az előrejelzések elvégzéséhez, értékeléséhez pedig egy tesztelő (validáló) minta (25%). A létrehozott modellek előrejelzési teljesítményének kiértékelése a tesztelő mintán elért összes helyes besorolás aránya és a ROC görbe alatti terület nagysága alapján történt.
A dolgozatban csak a tesztelési mintán elért eredmények kerülnek részletesen bemutatásra és elemzésre. (6. táblázat, 5. ábra)
Amint az előzetesen várható volt, mind a két modellezési eljárás igen pontos besorolást ért el a tesztelő mintán. A logisztikus regresszió a "normál" értékek esetében mindössze három, míg a "távolság" értékeket felhasználva négy változó alapján ért el 91,65%-os, illetve 94,06%-os összes helyes besorolási arányt. A "normál" értékeket tekintve az elsőfajú hiba aránya meghaladja a másodfajúét, ez arra enged következtetni, hogy a modell sikeresebben találja meg a csődös vállalatokat. A "távolság" értékeknél ez a reláció megfordul, hiszen minimális hibával találta meg a működő vállalatokat. A "távolság" értékek azonban összességében jobb teljesítményt nyújtottak, ezt az AUROC mérőszám is alátámasztja (0,991>0,968).
A neurális háló alapú modellek azonban még ennél is pontosabb besorolást eredményeznek. A "normál" értékek tekintetében a logit regresszióhoz képest minimálisan 1,2%p-tal javult az összes helyes besorolások aránya, ugyanakkor a másodfajú hibák aránya nőtt, ami azt jelenti, hogy a csődös vállalatokat kevésbé pontosan tudta megtalálni az eljárás. A minimális teljesítményjavulást az AUROC növekedése is mutatja. A "távolság" értékek alapján dolgozó neurális háló kiemelkedő telje-
6. táblázat: Az alapváltozós modellek teljesítménye
| Logisztikus regresszió | Neurális háló | |||
| "Normál" értékek | "Távolság" értékek | "Normál" értékek | "Távolság" értékek | |
| Elsőfajú hiba | 4,77% | 1,18% | 2,35% | 0,00% |
| Másodfajú hiba | 3,58% | 4,76% | 4,76% | 1,19% |
| Összes helyes besorolás | 91,65% | 94,06% | 92,89% | 98,81% |
| AUROC | 0,968 | 0,991 | 0,973 | 0,997 |
Forrás: saját szerkesztés
- 229/230 -
5. ábra: A logisztikus regresszió és a neurális háló ROC görbéi
a) ROC görbék a "normál" értékeken; b) ROC görbék a "távolság" értékeken

Forrás: saját szerkesztés
sítményt nyújtott, hiszen a 84 elemű tesztelési mintából mindössze egy vállalatot sorolt be tévesen. Az alapváltozókat felhasználó modellek közül ez bizonyult a legpontosabbnak, majdnem tökéletes besorolást ért el, amit alátámaszt a 98,81%-os összes helyes besorolási arány, valamint a 0,997-es AUROC érték is. A modell megtalálta az összes működő vállalatot, mindössze egy csődös vállalatnál hibázott. Erre az elsőfajú hiba hiányából lehet következtetni.
Összességében a "távolság" értékek használata minőségi javulást eredményezett, mind a két modellezési eljárásnál.
4. A faktorváltozókat felhasználó modellek értékelése
Az elvégzett faktoranalízisek eredményeképp az alábbi faktorokat sikerült azonosítani: jövedelmezőség, eszközgazdálkodás (-szerkezet), likviditás, tőkeszerkezet, növekedés, partner management. A modellkísérletek alapján a legfontosabb csődfaktorok a jövedelmezőség, likviditás és tőkeszerkezet, mind a "normál", mind pedig a "távolság" értékekre épülő modelleknél. (7. táblázat)
A faktorváltozók némileg pontatlanabb besorolást eredményeznek, mint az alapváltozókkal készített modellek. Ez leginkább a faktorok képzésének jellegéből adódik, hiszen az eljárás elsimítja a vállalatok közti különbségeket azáltal, hogy a pénzügyi mutatószámokat súlyozza. Ismert az a jelenség,[24] hogy a faktorizáció a klasszikus matematikai-statisztikai eljárások (ide tartozik a logisztikus regresszió is) teljesítményét növeli, azonban a szelektált, közvetlen versenytársak összehasonlítása érdekében kialakított mintán ez nem figyelhető meg. Itt is megfigyelhető azonban, hogy a neurális háló az összes helyes besorolások arányát tekintve job-
7. táblázat: A faktorváltozós modellek teljesítménye
| Logisztikus regresszió | Neurális háló | |||
| "Normál" értékek | "Távolság" értékek | "Normál" értékek | "Távolság" értékek | |
| Elsőfajú hiba | 10,71% | 4,77% | 4,77% | 2,38% |
| Másodfajú hiba | 4,76% | 4,76% | 7,12% | 1,19% |
| Összes helyes besorolás | 84,53% | 90,47% | 88,11% | 96,43% |
| AUROC | 0,952 | 0,981 | 0,960 | 0,990 |
Forrás: saját szerkesztés
- 230/231 -
ban teljesít, mint a logisztikus regresszió, mind a "normál", mind a "távolság" értékek esetében. Figyelemre méltó a "távolság" értékeken képzett faktorváltozókat felhasználó neurális háló 0,990-es AUROC értéke és a 96,43%-os helyes besorolási aránya. Ez azt jelenti, hogy a 84 elemű tesztelő mintán mindössze 3 vállalatot (2 működőt, 1 csődöst) sorolt be tévesen.
5. A modellek teljesítményének vizsgálata kétéves előrejelzési időtávon
Az eddig bemutatott előrejelzések a csődös állapot bekövetkezését megelőző üzleti év záró adatait használták fel, ezzel egyéves időtávú csőd-előrejelzéseknek tekinthetők. A csőd-előrejelzés gyakorlati alkalmazása során azonban gyakran felmerül az igény arra, hogy hosszabb távú előrejelzések készüljenek. Mivel a minta adatai a csődöt megelőző év beszámolóiból származnak, így ez lehetőséget nyújt a kétéves időtávú előrejelzések készítésére is.
A kétéves előrejelzések elkészítése a tesztelő minta adatainak lecserélésével történt a csődöt megelőző üzleti év beszámolóinak nyitóadataira A standardizálás és a trimmelés a csődöt megelőző utolsó év záró adatai alapján történt. A faktormodellek felhasználása nem volt lehetséges, mivel mind a két értéken képzett faktormodellben szerepel a növekedés faktor, ami kétévnyi adatot tartalmazó változókból épül fel. Ezért kétéves előrejelzések a faktormodellekkel nem készültek. (8. táblázat)
A korábban tárgyalt eltérések a "normál" és a "távolság" értékek, valamint a logisztikus regresszió és a neurális háló közt itt is helytállónak bizonyulnak. A neurális háló jobb teljesítményt nyújt a logisztikus regressziónál és a "távolság" értékek felhasználása javítja a modellek előrejelző-képességét a "normál" értékekhez képest, mind az összes helyes besorolások arányát, mind pedig a ROC görbe alatti területet figyelembe véve.
A kétéves előrejelzések készítésénél normális jelenségnek számít a modellek teljesítményének csökkenése, azonban a csökkenések mértékét érdemes alaposabban vizsgálni.
A legnagyobb visszaesést a "normál" értékeket felhasználó logisztikus regressziós modell esetében tapasztalhatjuk, hiszen a korábbi 91,65%-os helyes besorolási aránya 19,36%p-tal 72,29%-ra csökkent. Ez a modell rugalmatlanságát mutatja. A "távolság" értékeket felhasználó logisztikus regressziós modell szintén drasztikusan vesztett helyes besorolási teljesítményéből, csupán 82,93%-os arányt ért el, ami 11,13%p-os csökkenést jelent.
A "normál" értékeket felhasználó neurális háló is pontatlanabbá vált, 7,35%p-os csökkenés következett be. A "távolság" értékekre felépített neurális háló teljesítménye is csökkent, igaz a vizsgált modellek közül a legkisebb mértékben 7,14%p-tal és még így is kiemelkedő 91,67%-os pontossággal végezte a besorolást. A fentebb bemutatott hatások a ROC görbe alatti terület nagyságát vizsgálva is fennállnak.
A modellek teljesítményének romlása szinte minden esetben a másodfajú hiba emelkedésének köszönhető, ami azt jelenti, hogy nehezebben találták meg a modellek a csődös vállalatokat a csődöt megelőző második évben. A másodfajú hibák előfordulása a "normál" értékes logisztikus regressziónál volt a legnagyobb (22,89%), míg a "távolság" értékes neurális háló esetében csak minimálisan (+3,57%p-tal) emelkedett.
A fentiek alapján megállapítható, hogy a neurális háló rugalmasabb előrejelzési módszer, mivel teljesítménye kisebb mértékben romlott a logisztikus regresszióéhoz képest. A
8. táblázat: Az alapváltozós modellek teljesítménye kétéves előrejelzési időtávon
| Logisztikus regresszió | Neurális háló | |||
| "Normál" értékek | "Távolság" értékek | "Normál" értékek | "Távolság" értékek | |
| Elsőfajú hiba | 4.82% | 1.19% | 8.43% | 1.19% |
| Másodfajú hiba | 22.89% | 15.48% | 6.02% | 4.76% |
| Összes helyes besorolás | 72.29% | 82.93% | 85.54% | 91.67% |
| AUROC | 0,858 | 0,917 | 0,938 | 0,990 |
Forrás: saját szerkesztés
- 231/232 -
"távolság" értékek a vizsgálatok alapján jobban tompítják a modellek teljesítményének esését, tehát a versenytársaktól való lemaradásokat vizsgálva két évre előre is pontosabb előrejelzések készíthetők. Megint csak kiemelkedő teljesítményt mutat a "távolság" értékes neurális háló, mely összesen egy működő és három csődös vállalatot sorolt be tévesen a 84 elemű tesztelő mintában.
A mintába bekerült vállalatok beszámolóinak vizsgálata alapján három főbb ok vezethetett az előrejelzések pontosságának csökkenéséhez:
- a csőd, mint folyamat természetes lefolyása;
- a "kreatív" számviteli és egyéb jogi eszközök használata;
- a modellezési eljárások egyedi tulajdonságai.
A csődesemény bekövetkezése minden esetben egy hosszabb-rövidebb folyamat végeredményeképp adódik, ezért természetesnek tekinthető, hogy a csőd bekövetkezésének jelei két év távlatából halványabban látszanak, nem különülnek el olyan élesen a működő vállalatoktól.
A második ok a számviteli szabályok be nem tartásán, illetve szándékos félreértelmezésén alapszik. Ugyan a kirívó hibákat tartalmazó beszámolók kizárásra kerültek a vizsgálatból, mégis sok beszámoló tekintetében erős a gyanú, hogy nem a valós és hű képet mutatják a számok. Jellemző példa, hogy sok esetben éveken keresztül magas pl. a vevőkövetelések aránya, majd a csőd bekövetkezése előtt hirtelen lecsökken (többnyire értékvesztést számolnak el, illetve behajthatatlannak minősítik), míg ennek eredményhatása egyből drasztikusan lerontja az egyes eredménykategóriákat és ezáltal a jövedelmezőségi mutatókat. Ebben az esetben erős a gyanú, hogy az egyes évek során felhalmozódott értékvesztéseket nem a kellő időben, hanem a csőd előtt egy összegben számolták el. Lentner többször felhívja a figyelmet és kiemeli a vállalkozás folytatásának az elvének a maradéktalan teljesülését ami véleménye szerint csökkenti a vállalat gazdasági kockázatát, ezáltal távoltartja a csődhelyzeteket.[25]
Ugyancsak problémát jelent, hogy a csőd, illetve felszámolási eljárások megindítására sok esetben csak igen későn kerül sor. Mivel ezt a két eljárást a vállalkozástól független gazdasági szereplők kezdeményezhetik, így e szereplők megtévesztése, a vállalat valós gazdasági helyzetének eltitkolása komoly addicionális károkat okozhat.
A harmadik ok, amiért a modellek (elsősorban a logisztikus regressziós) teljesítménye csökken a modellek működési mechanizmusában és tulajdonságai közt keresendők. A logisztikus regresszió érzékeny a kiugró, extrém értékű adatokra. A csőd bekövetkezése előtti pillanatban (utolsó normális éves beszámoló tárgyévi adatai) már élesen elválnak a csődös és működő vállalatok, sok csődös vállalat pedig igen rossz állapotban van. Ugyan a kiugró adatok trimmelve lettek, mégis adódhatnak olyan nagy különbségek, amik két évvel hamarabb még csekélyebb mértékűek voltak. A logisztikus regressziós modell a csődöt megelőző, a csődös és működő vállalatok közt fennálló nagy eltérések időpontja alapján készült. Emiatt és az eljárás eredendő rugalmatlansága miatt a két évvel korábbi, még homogénebb állapotokat tükröző mintán nagymértékben csökken a teljesítménye. A neurális hálónál a kifinomultabb modellépítési (tanulási) algoritmus miatt ez a hatás kevésbé erősen jelentkezik. Zéman szerint minden vállalkozás működése során adódhatnak olyan kivételes helyzetek, hogy a megszokott módszerek helyett más megoldásokat alkalmazzon.[26] A pénzügyi controlling vezetéstámogató módszertanába feltétlenül szót kell ejteni a válságkezelés különböző esetéről mivel sokszor a hagyományos módszerek nem tudnak urrá lenni a pénzügyi feszültségeken, ezért a csődtörvény nem szokványos pénzügyi megoldásai követendők, amelyeket a kontrolling rendszerünk compliance követelményei közé kell sorolnunk. ■
JEGYZETEK
[1] Lásd pl. Fitzpatrick, Paul Joseph: A Comparison of the Ratios of Successful Industrial Entreprises with Those of Failed Companies. Accountants Publishing Company. Washington 1932. 21. o.
[2] Imre Balázs: Bázel II definíciókon alapuló nemfizetés-előrejelzési modellek magyarországi vállalati mintán, PhD. Értekezés, Gazdaságtudományi Kar, Miskolci Egyetem, Miskolc 2008.
[3] Maricica, M. - Georgeta, V.: Business failure risk analysis using financial ratios Procedia - Social and Behavioral Sciences, 2012. Vol 62, pp. 728-732.
[4] Altman, E. I.: Financial Ratios, Discriminant Analysis and the Prediction of Corporate Bankruptcy, The Journal of Finance,
- 232/233 -
1968. vol. 23: pp. 589-609,
[5] Bellovary, J - Giacomino, D. - Akers, M.: A Review of Bankruptcy Prediction Studies: 1930 to Present, [on-line] Journal of Financial Education. 2007. vol. 33 (winter), 2007
[6] Lásd: Kecskés A. - Halász V.: Társaságok a tőzsdén. HVG-Orac, Budapest 2011. és Kecskés A. - Halász V.: Stock Corporations - A Guide to Initial Public Offerings, Corporate Governance and Hostile Takeovers. HVG-Orac - LexisNexis, Budapest-Bécs 2013
[7] Altman, E. I. - Loris, B.: A financial early warning system for over-the-counter broker- dealers. The Journal of Finance. 1976. vol. 31 pp. 1201-1217.
[8] Altman E. I: Predicting financial distress of companies: revisiting the Z-score and ZETA® models. In: Handbook of Research Methods and Applications in Empirical Finance. Elgar, 2000. London 428-456. o.
[9] Zéman, Z. - Béhm, I.: A pénzügyi menedzsment controll elemzési eszköztára. Akadémiai Kiadó, Budapest 2016. 396. o.
[10] Ohlson, J. A.: Financial Ratios and the Probalistic Prediction of Bankruptcy, Journal of Accounting Research, 1980. Vol. 18, No.1, pp. 109-131.
[11] Frydman, H. - Altman, E.I. - Kao D.LI.: Introducing recursive partitioning for financial classification: the case of financial distress. Journal of Finance, 1985. Vol. 11. No. 5. 269-291. o.
[12] Odom, M.. - Sharda, R.: Bankruptcy prediction using neural networks. In: Proceedings of the IEEE International Conference on Neural Networks, San Diego 1990. pp. 133-168.
[13] Kristóf T.: Gazdasági szervezetek fennmaradásának és fizetőképességének előrejelzése, PhD. Értekezés, Jövőkutatás Tanszék, Budapesti Corvinus Egyetem, Budapest, 2008. 53. o.
[14] Balcean, S. - Ooghe, H.: Alternative methodologies in studies on business failure: Do they produce better results than the classic statistical methods?, Vlerick Leuven Gent Working Paper Series 2004/16
[15] Mures-Quintana M. J. - Garcia-Gallego, A.: On the non-financial information's significance in the business failure models. International Journal of Organizational Analysis. 2012. Vol. 20 No. 4, pp. 423-434.
[16] Zmijewski, M. E.. Methodological Issues Related to the Estimation of Financial Distress Prediction Models. Journal of Accounting Research, 1984. Vol. 22 Supplement, pp. 59-82.
[17] Kristóf: i.m.
[18] Ennek a kritériumnak a nem teljesítése okozta az építőipari, vendéglátó és ingatlanforgalmazó cégek kizárását.
[19] Azt a feltételezést a továbbiakban is fenn kellett tartani, hogy a könyvvizsgáló helyes véleményt mondott az adott évi beszámolóról, ugyanakkor mivel sok kirívóan hibás beszámolót is auditáltak, ez felvetheti a könyvvizsgálók és a cégbírósági ellenőrző rendszer felelősségét is.
[20] Fontossági sorrendben: árbevétel, mérlegfőösszeg, jegyzett tőke, mint a vállalkozás méretének mérőszámai
[21] Altrichter, M. - Horváth, G. - Pataki, B. - Strausz, Gy. - Takács, G. - Valyon, J.: Neurális hálózatok, [on-line] http://mialmanach.mit.bme.hu/neuralis/index, Panem Kiadó, 2006
[22] Kristóf: i.m.
[23] TVE, Total Variance Explained - A faktormodell által magyarázott összes variancia hányad
[24] Kristóf: i.m.
[25] Lentner Cs.: A vállalkozás folytatása számviteli alapelvének érvényesülése közüzemi szolgáltatóknál és költségvetési rend szerint gazdálkodóknál - magyar, európai jogi és eszmetörténeti vonatkozásokkal. In: Lentner Cs.: Adózási pénzügytan és államháztartási gazdálkodás. Közpénzügyek és Államháztartástan II. NKE Szolgltató Kft., Budapest 2015. pp. 763-783. valamint Lentner Cs. A vállalkozás folytatása számviteli alapelvéről. Gazdaság és Jog 2014. 22. (3) pp. 3-8
[26] Lásd Zéman, Z.: The Risk-mitigating Role of Financial Controlling at Local Government Entities: A pénzügyi controlling kockázatcsökkentő szerepe önkormányzati szervezeteknél. Pénzügyi Szemle 2017. (3) pp. 294-310 valamint Zéman, Z. - Hegedűs, Sz. - Molnár, P. Analysis of the Creditworthiness of Local Government-owned Companies with a Credit Scoring Method. Pénzügyi Szemle 2018. (2) pp.176-195.
Lábjegyzetek:
[1] A szerző hallgató, BGF Pénzügyi és Számviteli Kar, Számvitel MSc.
[2] A szerző főiskolai tanársegéd, BGF Pénzügyi és Számviteli Kar, Számvitel Intézeti Tanszék.
[3] A szerző egyetemi docens, SZIE Gazdaság és Társadalomtudományi Kar, ÜTI.

