Logika és jog (Markovich Réka, IJOTEN/Jogbölcselet, 180. szócikk, lezárás dátuma: 2023.05.14.)

Szerző: MARKOVICH Réka

Affiliáció: kutató tudós, Luxemburgi Egyetem, Department of Computer Science, Interdisciplinary Lab for Intelligent and Adaptive Systems, Faculty of Science, Technology and Medicine

Rovat: Jogbölcselet

Rovatszerkesztő: SZABÓ Miklós, JAKAB András

Lezárás dátuma: 2023.05.14.

Idézési javaslat: MARKOVICH Réka: "Logika és jog" in JAKAB András - KÖNCZÖL Miklós - MENYHÁRD Attila - SULYOK Gábor (szerk.): Internetes Jogtudományi Enciklopédia (Jogbölcselet rovat, rovatszerkesztő: SZABÓ Miklós, JAKAB András) http://ijoten.hu/szocikk/logika-es-jog (2023). Konkrét szöveghelyre való hivatkozáshoz javasoljuk a szövegbeli bekezdésszámok használatát, pl. [8] vagy [12]-[18].

A formális logika a helyes következtetés, bizonyítás, érvelés formális tudománya, az igazság megismerésének és a tudományos megismerésnek a módszertana. A jogra vagy jogban való alkalmazhatósága és alkalmazandósága gyakran vita tárgya, számos jogelméleti (és logikafilozófiai) kérdést vet fel. Az alkalmazhatóság, sőt alkalmazandóság mellett érvelők szerint a formális logika a jogban egyrészről alkalmas a jogi érvelés, következtetés tanulmányozására és kritikai elemzésére, másrészről pedig - ezzel összefüggésben - a jogban használt fogalmak pontos jelentésének, a jogszabályok pontos tartalmának a feltárására, az esetleges ellentmondások kiszűrésére. Ezek a vizsgálatok egyben előfeltételeit is jelentik annak, hogy a mesterséges intelligencia számos eszköze alkalmazható legyen a jogra; így nemcsak jogi informatikai alkalmazások fejlesztése szempontjából kritikusak, hanem szükségesek a (majdan létrejövő autonóm) mesterséges ágensek jogi fogalmakkal és normákkal való érvelési-következtetési képességének megalapozásához is.

1. Logika és jog? Normákról és igazságról

[1] A ma ismert formális logika mint diszciplína egyrészt a(z analitikus) filozófiához, másrészt a matematika alá tartozik. Ha szét szeretnénk választani az - egyébként nem élesen különváló - filozófiai logikát és a matematikai logikát, akkor fogalmazhatunk úgy, hogy az előbbi a gondolkodás (gondolatmenet), érvelés elemzésének - és kritikájának - eszköze, amelyhez matematikai modelleket építünk. E matematikai modellek önmagukban való vizsgálata a matematikai logika tárgya, míg a filozófiában ezeket a modelleket használjuk, a használat célja, az alkalmazás tárgya szerinti rendszert törekszünk építeni: ezek adekvátsága tehát a matematikai elvárásokon túl az adott tárgyra való alkalmazhatóságuktól függ.

[2] Következtetés alatt olyan gondolatmenetet értünk, amelyben a rendelkezésre álló információkból, állításokból megfogalmazunk egy másik, "új" állítást: újat abban az értelemben, hogy eddig nem képezte expliciten a tudásunk részét, nem újat azonban abban az értelemben, hogy a rendelkezésre álló tudásunkon kívül nem használtunk fel új információt, pusztán a meglévőkből jutunk erre az újra. Egy ilyen gondolatmenet helyessége az állítások igazsága közötti összefüggésen múlik. Azt nevezzük helyes (vagy más szóhasználatban: érvényes) következtetésnek, amikor a kiinduló állítások, ún. premisszák igazsága biztosítja azt, hogy az "új" állításunk, az ún. konklúzió igaz legyen; az igazságnak ez az átörökítődése jelenti a helyes következtetést. Fontos érteni, ez annyit jelent, hogy amennyiben a premisszák igazak, úgy a konklúzió is az: a helyesség fogalma nem függ attól, hogy tényleg igazak-e a premisszáink - ez ugyanis nem logikai kérdés -, csak az összefüggést vizsgálja. Ha tényleg igazak a premisszáink, és ennélfogva a konklúziónk is az lesz, azt konkluzív következtetésnek hívjuk. Az elnevezés arra utal, hogy az így kapott állítás, a konklúzió bizonyosan igaz, az információtartalmát valóban "használhatjuk", arra építhetünk. Az, hogy az igazság milyen állításokról milyen állításokra örökítődik át (azaz a következtetésünk helyessége), az állítások szerkezetétől függ. Az pedig, hogy konkluzív-e, az állítások szerkezetén túl (hiszen az érvényesség kell a konkluzivitáshoz) az állítások tartalmán múlik, azon, hogy azok hogyan viszonyulnak a valósághoz: igazak-e. Egy természetes nyelvi állítás szerkezete nem mindig világos első ránézésre (néha sokadikra sem); ezért is használunk a természetes nyelv helyett valamilyen formális nyelvet, amelyben már nincs jelen a természetes nyelvet gyakran jellemző homályosság, kétértelműség: a formális nyelvben használt kifejezésekhez, jelölésekhez rendelt jelentés világos, előre rögzített.

[3] A logika jogra-jogban való alkalmazhatóságát illető egyik - ha nem a - legalapvetőbb kérdést Jørgen Jørgensen 1937-ben fogalmazta meg; felvetése Jørgensen-dilemmaként híresült el.[1] A dilemma abból adódik, hogy a logika állítások közötti kapcsolatot vizsgál, az állításoknak pedig alapvető tulajdonsága, hogy ún. igazságértékkel bírnak: igazak vagy hamisak. A jog viszont nem állításokkal, hanem előírásokkal, normákkal (->jogi normatan) operál: ezek, nem leíró, hanem előíró jellegűek (még ha a természetes nyelvi megjelenésük nem felszólító módban, hanem kijelentő mondat formájában történik is), vagyis se nem igazak, se nem hamisak. Ennek megfelelően, a logika - elvileg - nem alkalmazható a jogra, annak normáira, a normák közötti összefüggésekre. Mindazonáltal, érvel Jørgensen, az is nyilvánvalónak tűnik, hogy egy jogi következtés vagy érv(elés) premisszái és konklúziója között sem esetleges az összefüggés: a jogalkalmazás maga is következtetési folyamatnak tűnik, amit ráadásul évezredek óta sikerrel alkalmaznak.

[4] Vegyük például a Polgári Törvénykönyv híres kártérítési (->károkozás és kártérítés) szabályát: 6:519. § "Aki másnak jogellenesen kárt okoz, köteles azt megtéríteni." Ennek a szabálynak a logikai rekonstrukciója egy ún. kondicionális: "ha valaki másnak jogellenesen kárt okoz, akkor köteles azt megtéríteni". A vonatkozó névmás használatával[2] és a bárminemű szűkítés hiányával a jogalkotó általánosságot jelöl: bárki, mindenki, aki másnak jogellenesen kárt okoz, köteles azt megtéríteni. Ez az ún. elsőrendű logikában egy univerzális kvantorral és egy változóval jelölhető, amivel a logikai szerkezet a következőképpen néz ki: minden x-re (igaz az, hogy) ha x másnak jogellenesen kárt okoz, akkor x köteles azt megtéríteni. A bírósági eljárás során megállapítást nyer, hogy valaki - egy konkrét személy, akit az a ún. konstans individuumnévvel jelölhetünk - másnak jogellenesen kárt okozott. A bíró, alkalmazva a Ptk. kártérítési szabályát, úgy rendelkezik, hogy a köteles a kárt megtéríteni. Vagyis a következőképpen néz ki a következtetés:

• Premissza 1: minden x-re (igaz az, hogy) ha x másnak jogellenesen kárt okoz, akkor x köteles azt megtéríteni

• Premissza 2: a másnak jogellenesen kárt okozott

• Konklúzió: (Tehát) a köteles a kárt megtéríteni.

[5] Azt a következtetést, amelyben az egyik premissza egy kondicionális állítás, a másik a kondicionális előtagja (a "ha" kötőszóval bevezetett tagmondat), a konklúzió pedig a kondicionális utótagja (az "akkor" kötőszóval bevezetett tagmondat), modus ponensnek hívjuk, és a legalapvetőbb, leggyakoribb, legközkeletűbb következtetési forma. Csakhogy a fenti "következtetésben" Premissza 1 és a Konklúzió nem állítások, hanem előírások, normák: egy általános és egy konkrét norma. Vagyis, szemben Premissza 2-vel, nem lehetnek igazak vagy hamisak. Márpedig a modus ponens "működése" azon alapszik, hogy amennyiben egy kondicionálist igaznak fogadunk el, úgy az előtag igazságából következik az utótag igazsága. De ha elfogadjuk, hogy a normák nem lehetnek igazak vagy hamisak, akkor vagy el kell vetnünk, hogy a jogi "következtetésben" logikai megfontolás mentén fogadunk vagy nem fogadunk el egy konklúziót, vagy azt kell mondanunk, hogy a normáknak van logikája (a normákra alkalmazható valamilyen logika), de az nem az igazságértéken alapul.

[6] Solt Kornél a Jog és logika című könyvében[3] Ota Weinberger válaszalternatíváit[4] veszi számba:

1. ki kell terjeszteni a következtetési eljárás szabályait úgy, hogy normákra is alkalmazhatók legyenek,

2. le kell fordítani, redukálni kell a normákat állításokra, vagy

3. bele kell nyugodni, hogy nincsenek olyan érvényes logikai következtetések, amelyeket normákra is alkalmazhatnánk.

Az utolsó verziót maga Weinberger sem tartotta valódi megoldásnak, a b)-ről pedig azt mondta: "...a normák egyenértékű lefordítása állításokra eddig nem sikerült, és e tekintetben alig van kilátás a sikerre". Így szerinte egyedül az a) verzió lehet megoldás. Ennek keretében szimplán analógiát kell alkalmaznunk az igaz-hamis megkülönböztetés és a (jogilag) érvényes-érvénytelen distinkció között. Ezzel kvázi kiterjeszthetjük a következtetés szabályait - csakhogy mindössze a "tiszta" normakövetkeztetésekre. Azoknak következtetéseknek a problémája, amelyek normát is és állítást is tartalmaznak, továbbra sincs megoldva.

[7] Solt rekonstrukciója szerint 1951-ben Georg von Wright a b) megoldásra építve alapozta meg azt, amit deontikus logikának hívunk.[5] A deontos görög szó, nagyjából úgy fordítható le, hogy 'kell', 'kellene'. A deontikus logika pedig, ennek megfelelően, a normák, normatív rendszerek logikája. Pontosabban logikái, hiszen a "deontikus logika" egyes számban gyűjtőnév: sokféle deontikus logika van, azaz olyan formális rendszer, amely ezeket a jelenségeket "kezeli". Az a rendszer, amit von Wright az 1951-es, Deontic Logic című cikkben lefektetett, nagyon közel van ahhoz, amit sztenderd deontikus logikaként ismerünk.[6] Von Wright valóban igaz-hamis állításokként (proposition) kezeli az OA típusú mondatokat, ahol az A egy cselekménytípust jelöl, az O pedig a kötelezőséget jelölő ún. modális operátor (az ought, illetve obligatory szavak kezdőbetűjéből), a szándékolt jelentése a mondatnak pedig az, hogy az A cselekmény kötelező. (Von Wright a cselekményekhez az igazságértékkel szigorúan analógnak tekintett végrehajtásértéket rendel, de egyszerűbb erre úgy gondolni, hogy az A egy állítás arról, hogy az adott cselekmény végre van hajtva, és akkor közvetlenül beszélhetünk igazságértékről. Később az is vált általánossá, hogy állításokra, és nem cselekményekre alkalmazzuk az operátort: Op szándékolt jelentése az, hogy 'kötelező, hogy az legyen a helyzet, hogy p', ahol p tetszőleges propozíció.) Von Wright a megengedettséget (permitted, P) vette definiálatlan alapkategóriaként és ebből határozta meg a többi modális operátort: tilos (forbidden, F) az a cselekmény, amit nem megengedett végrehajtani, kötelező az a cselekmény, amit nem megengedett nem végrehajtani; logikai szimbólumokkal: FA = ~PA és OA = ~P~A (a ~ a negáció, a = az ekvivalencia jelölése, ez utóbbi azt jelenti, hogy a két oldalon álló formula ugyanolyan feltételek mellett igaz).

[8] Egy adott logika (logikai rendszer) három elemből épül fel: (i) van egy formálisan specifikált nyelve: ez adja meg, hogy melyek az ún. jól formált formulái a nyelvnek (mi az ábécéje, mik a mondatai), (ii) a formulák interpretációját, igazságfeltételeit a szemantika adja meg (jellemzően egy másik formális elméletet, például halmazelméletet használva), (iii) a formulák közötti levezetési szabályokat pedig a kalkulus (szintaxis).[7] Egy állítás igazságfeltételei tehát a szemantikán múlnak. Von Wright nem dolgozott ki szemantikát a rendszereihez, viszont az ő 1951-es rendszerével csaknem azonos sztenderd deontikus logikához használt ún. lehetségesvilág-szemantika úgy oldja meg, hogy a preskripciókhoz igazságértéket kapcsoljon, hogy az O operátor hatókörében lévő állítást a (jogilag) ideális világokban értelmezi igaznak: akkor igaz az aktuális világban, hogy Op, ha p az összes jogilag ideális világban igaz.[8]

[9] Von Wright későbbi műveiben felülvizsgálja a Deontic Logicban vázolt megközelítést. Az 1963-ban megjelent Norm and Action című monográfiában[9] kifejt egy új rendszert (new system), amelyben egyrészt egy sokkal kimunkáltabb cselekményreprezentációra épít (állapotok közötti változásokat és azok előidézését leíró mondatokra alkalmazza az operátort), másrészt hosszasan elemzi a deontikus logikában kezelni kívánt megnyilatkozások kettős természetét. Annak a megnyilatkozásnak, hogy "a ház előtt parkolni megengedett" van egy preskriptív olvasata: ha az mondja, aki jogosult dönteni arról, hogy lehet-e parkolni az adott ház előtt; és van egy deskriptív olvasata: ha bárki más ezt a megengedést "hivatkozza". Von Wright ekkor már úgy véli, igazságértéket csak ez utóbbihoz tudunk rendelni, így csak az ún. normapropzíciókra (deskriptív olvasat) alkalmazott logika épülhet erre, a normák (preskriptív olvasat) logikája nem, de a két rendszer teljesen párhuzamos. Később még radikálisabb nézetre jut: 1991-ben úgy vall erről, volt, amikor - Kelsen híres álláspontjához hasonlóan -[10] azt gondolta, nem is lehetséges a normalogika.[11] Pályája végére mérsékeltebb álláspontot foglal el: arra jut, hogy a normák logikáját nem az igazságértékre és annak öröklődésére kell építeni, hanem a racionalitásra: lehet egymásnak ellentmondó (jog)szabályokat alkotni, de az irracionális, minthogy a norma címzettje valódi ellentmondással találná szemben magát, ha megpróbálná azokat (egyszerre) követni.

[10] Míg a deontikus logika modális logikaként (azaz modális operátorok használatára épülő rendszerként, ahol ezekhez a modális állításokhoz igazságértéket tudunk rendelni) való kezelése a mai napig tartja magát, sőt mi több, általánosnak mondható, néhány logikust nem hagyott nyugodni a Jørgensen-dilemma. David Makinson az A Fundamental Problem of Deontic Logic című cikkében[12] kezdeményezte egy olyan rendszer kidolgozását, amely Carlos Alchourrón és Eugenio Bulygin - Erik Stenius egy korábbi esszéjén[13] alapuló - munkáját[14] viszi tovább. Ez a megközelítés normatív rendszerekről beszél; nem a normákhoz rendel igazságértéket, hanem ahhoz az állításhoz, hogy egy adott normatív kódexnek eleme-e egy adott norma.

[11] Ebből a kezdeményezésből nőtte ki magát az ún. input-output logika (IOL), ami a feltételes normáknak egy meglehetősen absztrakt megközelítését adja. Úgy tekint a normatív rendszerekre, mint Boole-formulák (konjunktív, diszjunktív, negált formulák) között fennálló relációk halmazaira: (a,x) rendezett párokkal dolgozik, amelyekben a és x is formula, a szándékolt jelentés pedig az, hogy a fennállása esetén x kötelező. Ha egy normatív rendszer, amely tartalmazza az (a,x) normát, az a formulát megkapja inputnak (vagyis, hogy ha a a helyzet), akkor az output - ami azt adja meg nekünk, hogy mi adott helyzetben a kötelező - tartalmazza x-et: ez az ún. factual detachment, az input-output logika központi művelete, ami így anélkül teszi lehetővé a modus ponens használatát (egy feltételes normából és annak az előtagjából levezeti nekünk az utótagot), hogy belefutnánk a Jørgensen-dilemmába.

[12] Ez az absztrakció első látásra talán megnehezíti annak elképzelését, hogy a formális logika a jogra közvetlenül alkalmazható (például mert nem látjuk sem szintaktikai, sem szemantikai nyomát a jogban használt deontikus modalitásoknak). Valójában azonban egy nagyon intuitív és könnyen variálható rendszert hoz létre, amelyben számos verzió közül választhatunk aszerint, hogy milyen axiómák és levezetési szabályok kombinációját látjuk megfelelően egyensúlyozni az intuícióink és a konzisztens rendszer követelménye között.

2. Egyéb lehetséges ellenvetések a logika jogban/jogra való használhatóságával szemben

2.1. Jogi érvelés vs. deduktív érvelés

[13] Gyakran felmerülő érv a logika használata ellen, hogy míg a formális (vagy szimbolikus) logika a deduktív érvelés, következtetés tudománya, addig a jogban nem vagy nem kizárólag deduktív érvelést alkalmazunk (->jogi érveléselmélet). Az érvelés vagy az érvek tárgyalásakor valóban meg szokás különböztetni deduktív és induktív érvelést, és szokás beszélni analógiás és abduktív érvelésről is. A dedukció az általánosból az egyedi levezetését jelenti, a deduktív érvelés pedig azokat a következtetéseket, amelyeknél a premisszák igazsága biztosítja a konklúzió igazságát (egészen idáig mi magunk is ennek keretében tárgyaltuk a logikát, logikai levezetésről beszéltünk). Az induktív érvelésben ehhez képest a premisszák csak valószínűsítik a "konklúzió" igazságát: a jellegzetes induktív következtetés az egyediből általánosra való "következtetés" (illetve erre való törekvés, ha a "következtetés" szót a biztosan működő, deduktív következtetésre tartjuk fenn).[15] A mindennapi életben kifejezetten nagy szerepe van az induktív "következtetéseknek": a világról alkotott képünk hiányos, a tudásunk sporadikus, a rendelkezésre álló információkból próbálunk következtetni, még ha tudjuk is, hogy ez nem jár biztosan igaz konklúzióval. Az analógiás érvelés két jelenség közötti hasonlóság alapján törekszik további hasonlóságok állítására (feltételezésére), míg az abdukciós érvelésben egy jelenség legvalószínűbb magyarázatára próbálunk "következtetni".

[14] Henry Prakken naiv deduktivizmusnak nevezi azt az - ebben a leegyszerűsített formában lényegében senki által sem vallott - nézetet, hogy a logikát a jogban/a jogra/a jog elemzésében lehet/kell használni, mert a jogi érvelés deduktív érvelés.[16] Támadni, ezzel szemben, sokan támadják, hangsúlyozván, hogy a jogi érvelés nem vagy nem csak deduktív érvelés.[17] Ez valóban így van: a jogban tényleg mindegyik érveléstípus szerepet játszik, elég csak a common law rendszerekben (->a common law jogrendszerek) csaknem egyeduralkodó, de a civil law országokban is meghatározó eset- és precedensalapú érvelésre gondolni (->precedens). Csakhogy annak hirdetése, hogy a logika használata a jog, a jogi érvelés elemzésében, modellezésében hasznos, nem jelent elköteleződést a naiv deduktivizmus mellett.

2.2. Defizibilitás

[15] A hiányos információk és a következtés igényének összeegyeztethetőségére való törekvés hívta életre az ún. defizibilis logikát, amelynek a jog szempontjából kiemelt jelentősége van. A klasszikus logikának meghatározó tulajdonsága, hogy monoton: a premisszák bővítése nem befolyásolja a kiinduló premisszákból levont következtetés érvényességét. A jogban azonban a legtöbb következtetés - ahogy Szabó Miklós magyarul fogalmaz[18] - megtámadható: a ->bizonyítás során például az újonnan feltárt bizonyítékok fényében az ellenkezőjére fordulhat a konklúzió a bűnösségről. De a jogrendszerek szerkezetét is sokan tekintik - a konklúziót megváltoztató - kivételekkel terheltnek, így defizibilisnek: H. L. A. Hart az elsők között hívta fel a figyelmet a pozitív feltételek mellett a teljesülést aláásó tényezők jelentőségére a jogi következtetés szempontjából.[19] A defizibilitás (esendőség) (jogi) logikába való beépítése megoldást jelenthet ennek a kifogásnak a kiküszöbölésére.[20] Szabó Miklós a nem formális logikák között beszél a nemmonoton logikákról,[21] s bár ezen formális rendszerek különbözősége a klasszikus logikáktól valóban felvet számos logikafilozófiai kérdést, megannyi formális rendszer, logika létezik, amely beépíti valamilyen módon a defizibilitást,[22] valamint a komputációs argumentációt (computational argumentation) mint külön formális rendszert is nagyon gyakran használják jogi struktúrák modellezésére, részben éppen a nemmonoton karaktere miatt.[23]

2.3. Formalizálás mint az interpretáció lehetőségének kizárása

[16] Prakken tárgyalja azt a nézetet is, amely szerint a logika azért nem adekvát eszköz a jog modellezésére, mert a formalizálás a jelentés olyan pontos meghatározását jelenti egy fogalomnak, amely kizárja a jogba szándékosan belefoglalt interpretációs mozgásteret - és Philip Leith szerint ezzel a jogalkalmazók szerepét veszi át, ami problémás.[24] Ezt az aggodalmat érdemes először szintaktikai oldalról megvizsgálni: egy állítás (norma) - mint mondat - formalizálása valóban meghatároz egy logikai szerkezetet; egy "ha..., akkor..." megfogalmazású állítást például jellemzően kondicionálisként reprezentálunk. A kondicionális - mint valamennyi logikai konnektívum - ún. igazságfüggvény: az igazságfüggvények összekapcsolások, amelyek azt határozzák meg, hogy a tagmondatok igazsága hogyan hat az összetett mondat igazságára. Azért nevezzük ezeket függvényeknek, mert egyértelműen meghatározzák az adott bemenethez tartozó kimenetet. Egy kondicionális állítás például csak egy módon lehet hamis: amennyiben az előtagja igaz, az utótagja pedig hamis, vagyis ha az előtagban foglalt feltétel elégséges. Egy norma esetén ez azt jelenti, hogy az előtagban foglalt feltétel fennállása esetén az utótagban foglalt kötelezés, tilalom vagy megengedés is fennáll. Elképzelhető, hogy más feltételek esetén is, de az ebben a normában foglalt feltétel fennállta, megvalósulása önmagában elégséges a norma rendelkező részének alkalmazandóságához.

[17] Nem a kondicionális azonban az egyetlen konnektívum, amelyre a feltételes állítások (normák) lefordíthatók. Az ún. konverz kondicionális (vagy retrokondicionális) épp a szükséges feltételeket megadó logikai állításforma. Ez is egy módon lehet hamis: akkor, ha a feltétel (a "ha"-val bevezetett tagmondat) hamis, míg a másik tagmondat igaz. A természetes nyelven történő megnyilatkozások esetében jellemzően nem teljesen biztos, hogy a megnyilatkozó szükséges vagy elégséges feltételt jelöl meg egy olyan mondattal, amelyben "ha" kötőszóval és "akkor" kötőszóval bevezetett tagmondatok szerepelnek.[25] Ráadásul, a bikondocionális is egy lehetséges logikai konnektívum: az az eset, amikor a megjelölt feltétel szükséges és elégséges is egyben. Az "akkor és csak akkor, ha..." kifejezés pontosan megjelöli ugyan, hogy erről és nem a kondicionálisról vagy a retrokondicionálisról van szó, ez azonban - jellemzően - csak matematikai szabatosságú szövegekben használatos.

[18] Egy feltételes mondat - ami a jogban meglehetősen gyakori - tehát elvileg háromféle logikai szerkezetet takarhat,[26] és amint formalizáljuk ezeket a normákat, választunk közülük: egy verzió marad.[27] A "vád" tehát, hogy a formalizálás elveszi az interpretáció lehetőségét, szintaktikai értelemben megáll. Kérdés azonban, egyrészt, hogy a szintaxist illetően nyitva hagyott interpretációs lehetőség valóban szükséges-e a jogban, és hogy - amennyiben az -, van-e a logikának, pontosabban a logikai modellezés módszerének megoldása erre.

[19] Az utóbbi kérdést illetően Trevor Bench-Capon és Marek Sergot,[28] valamit Layman Allen és Charles Saxon[29] is tárgyal olyan jogi tudásbázisú rendszereket (knowledge-based systems), amelyekben több alternatív - szintaktikailag különböző - lehetséges formalizálás szerepel, tehát a formalizálás nem szükségszerűen jelent elköteleződést. Az előbbi kérdésre pedig, miszerint jó-e az, hogy a szintaxist illetően is van tere az interpretációnak, érdemes a jogszabályszerkesztésről szóló IRM rendelet[30] egy szakaszát felidézni, amelyben a jogalkotó - egy felsorolás elemei között és néhány kötőszó tekintetében legalábbis - egyértelműséget követel a (szintaktikai) logikai viszonyokat illetően:

7. § (1) Felsorolás alkalmazása esetén egyértelművé kell tenni, hogy a felsorolás elemei közül

a) valamennyinek teljesülnie kell,

b) egyik sem teljesülhet,

c) pontosan egynek kell teljesülnie vagy

d) legalább egynek teljesülnie kell

(a továbbiakban: a felsorolás elemei közötti logikai kapcsolat) a joghatás kiváltásához.

(2) A felsorolás elemei közötti logikai kapcsolatot

a) a mondatnak a felsorolást megelőző vagy követő szövegrészében,

b) a felsorolás utolsó előtti eleméhez fűzött kötőszóval,

c) - ha a b) pont nem alkalmazható - a felsorolás több eleméhez fűzött kötőszóval vagy

d) a felsorolástól különálló mondatban

kell megállapítani.

(3) Az "illetve" kötőszó jogszabály tervezetében csak más egyértelmű nyelvi megfogalmazás alkalmazhatatlansága esetén alkalmazható.

(4) Az "illetőleg" kötőszó a jogszabály tervezetében nem alkalmazható.

(5) Az "és" és a "vagy" kötőszó írásjellel összekapcsolva vagy közvetlenül egymást követően a jogszabály tervezetében nem alkalmazható.

Ez a követelmény azt sugallja, hogy a szintaktikai többértelműség nem kívánatos. A jogalkotó eszerint tiltja a szándékosan nyitva hagyott teret az interpretáció ezen formája számára - legalábbis a nevesített viszonyokat és helyzeteket illetően. Ez természetesen nem jelenti azt, hogy nem marad többértelmű szerkezet a jogszabályokban (lásd a fenti problémát a feltételes szerkezetekkel), és ha marad, azt nyilván a jogalkalmazó dolga értelmezni az adott jogrendszer dogmatikájában megjelölt ->értelmezési módszerek, elvek szerint.

[20] Az a vád, hogy a formalizálás kizárja az interpretáció lehetőségét, érthető szemantikai szinten is: mégpedig a jogszabályban használt fogalmak "túlzott" definiálására. Bár számos logikai kutatás célozza kifejezetten az egyes jogi fogalmak komputációs struktúrájának (következményeinek) a feltárását, önmagában az, hogy a jogszabályok modellezésére logikát alkalmazunk, nem kényszeríti ki a fogalmak definiálását: abból az összefüggésből, hogy ha kötelező adót fizetni, akkor megengedett adót fizetni, nem következik semmi az adó fogalmának tartalmát illetően. Az adott logikai rendszer szemantikájában természetesen valahogy interpretálva lesz az adófizetés ténye, de ez csak annyit jelent, hogy mint állításhoz igazságértéket tudunk hozzá kapcsolni: az adó jelentését illetően semmilyen elköteleződést nem vállalunk. Vagyis szemantikai értelemben még annyira sem áll meg a vád, mint a szintaxist illetően.

[21] Mindazonáltal több jogszabály együttes formalizálása esetén felmerülhet például a kérdés, hogy a különböző jogszabályokban előforduló - szóalakra azonos - fogalmakat ugyanúgy (például ugyanannak az individuumnévnek) reprezentáljuk-e. A kapcsolódó jogszabályokat illetően a jogszabályszerkesztésről szóló IRM rendelet rögzít olyan legisztikai elvárást, amely az ebbéli mozgástér lehetőségét elvileg kizárja,[31] de a nem kapcsolódó jogszabályokra ilyen előírás nincs, így ott különös körültekintéssel kell eljárni a formalizáláskor.

3. Modális logika, deontikus és jogi modalitások, valamint a jogi nyelvben használt modalitások

[22] Mivel a sztenderd megközelítések a jogra még mindig leginkább a deontikus logikát mint modális logikát alkalmazzák, érdemes megvizsgálni a deontikus logika modalitásait a jogi modalitások és azok beazonosíthatósága fényében. A modális logika szűkebb értelemben a szükségszerűséget, lehetségességet, lehetetlenséget kifejező állítások logikája. Szimbolikus logikaként való kidolgozását C. I. Lewishoz szokás kötni. A klasszikus logikának olyan kiterjesztését jelenti, amelyben az adott modalitások szimbólumai is szerepelnek, ún. operátorokként: a □ (box) szimbólum a szükségszerűséget jelöli, a ◊ (diamond) a lehetségességet. Ezeket az operátorokat állításokra alkalmazva modális állításokat kapunk, amelyek igazsága így már nem "számítható ki" az állítások tagmondatainak igazságából (ahogyan a klasszikus logikában), mivel azok jelentésétől (intenziójától) is függ: a modális logika tehát ún. intenzionális logika.

[23] A modális operátoroknak azonban számos további értelemzése is lehetséges a szükségszerűségen és a lehetőségen túl: az episztemikus értelmezés a tudás (tudottság) modalitással operál, a doxasztikus a hit (hittség) modalitással, a temporális az időt illető modalitásokkal (például valami igaz volt, igaz lesz, mindig igaz volt, mindig igaz lesz), a deontikus pedig a kötelezőséggel és megengedettséggel.[32] Modális logikán tágabb értelemben az összes, ilyen értelmezés mentén létrejövő logikai rendszert értjük; a kiindulópontként szolgáló metafizikai modalitások - a szükségszerűség és a lehetségesség - logikájára pedig alethikus logikaként szokás hivatkozni. A különböző modális rendszereket az választja el, hogy milyen axiómákból építhető fel az adott értelmezésnek megfelelő formális rendszer: milyen mindenképpen igaznak tekintett alapállításokból tudunk azokra a tulajdonságokra következtetni, amelyeket intuitíven igaznak érzünk az adott modalitások viszonylatában.

[24] Az alethikus modalitások egymás közötti logikai viszonyait ábrázolja a modális hatszög:[33]

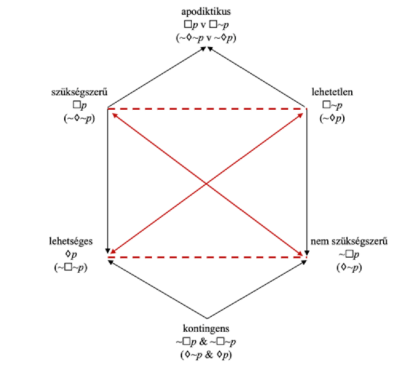
1. ábra

Modális hatszög. Az arisztotelészi négyszöget dolgozta át egy időben (de egymástól függetlenül) két francia logikus, Robert Blanché és Augustin Sesmat

Az ábrán a különböző vonalak és nyilak az egyes modalitások (modális állítások) közötti logikai viszonyokat jelzik. A fekete nyíl következményrelációt jelöl: abból például, hogy valami szükségszerű, következik, hogy lehetséges; ahogyan a lehetetlenségből is következik, hogy nem szükségszerű. A folyamatos piros nyíl kontradiktórikus viszonyt jelöl: nem lehet egyszerre sem igaz, sem hamis, hogy valami (egy állítás igazsága) szükségszerű és nem szükségszerű; ugyanez áll a lehetséges-lehetetlen viszonyra. A szaggatott piros vonal ellentétes viszonyt jelent az ábrán: az ellentétes viszonyok egyik oldalán álló modális státusz igaz p-re, akkor és csak akkor a másik oldalon lévő státusz ~p-re igaz. Az apodiktikus státusz azt jelenti, hogy valami (egy állítás) vagy szükségszerű, vagy lehetetlen, míg a kontingensség esetlegességet jelent, vagyis annyit tesz, hogy egyszerre igaz valamiről, hogy nem szükségszerű és hogy lehetséges. Vagyis az esetlegesség szűkebb fogalom, mint a "lehetséges", hiszen ami szükségszerű, az lehetséges, viszont az épp nem áll rá, hogy kontingens lenne (hiszen itt a fogalom része nem szükségszerűnek lenni, és a szükségszerűség és a nem szükségszerűség között kontradiktórikus a "kapcsolat").

[25] A kötelezőséget és megengedettséget modalitásként, egész pontosan jogi modalitásként értékelte már Gottfried Wilhelm Leibniz is: 1672-es Elementa juris naturalis című művében négy jogi modalitást különített el: debitum (kötelező) - licitum (megengedett) - illicitum (tilos) - indifferentum (közömbös).[34] Ezeket a modalitásokat kiegészíthetjük további kettővel, hogy a deontikus modalitásokból is hatszöget alkothassunk:

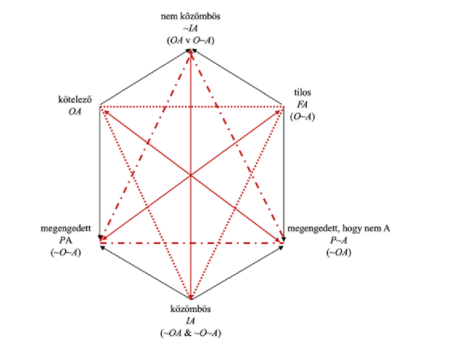
2. ábra

Deontikus hatszög[35]

Ha egy A cselekvés kötelező, abból következik, hogy megengedett, és az is, hogy nem közömbös. Ha egy cselekmény közömbös, akkor megengedett, ahogyan az is, hogy tartózkodjunk tőle. Ha pedig egy cselekmény tilos, abból következik, hogy megengedett, hogy tartózkodjunk a végrehajtásától. A piros nyilak kontradiktórikus viszonyt jelölnek az állítások között, azaz pontosan akkor igaz az egyik állítás, amikor hamis a (nyíl másik végén elhelyezkedő) másik. A pöttyözött vonalak kontrárius viszonyt jelölnek, vagyis az állítások lehetnek egyszerre hamisak, de nem lehetnek egyszerre igazak; a szaggatott-pöttyözött vonalak pedig szubkontrárius viszonyt, azaz a végeiken elhelyezkedő formulák (azaz az állítások, amelyeket reprezentálnak) lehetnek egyszerre igazak, de hamisak nem.[36]

[26] A kirajzolódó párhuzamok ellenére lényeges eltéréseket találunk a két rendszer között: ezek adják a deontikus logikának a modális logikák közötti karakterisztikáját. A két legfontosabb, intuíciónk alapján is világos különbség a következő. Egyrészt, míg a klasszikus modális logikában áll, hogy ami szükségszerűen igaz, az igaz, vagyis, hogy □A->A (ezt nevezzük alethikus sémának vagy T axiómának), addig nyilvánvaló, hogy attól, hogy egy cselekmény kötelező, korántsem biztos, hogy végre is hajtják, vagyis nem teljesül, hogy OA->A. Ehelyett annyit állíthatunk csupán, hogy OA->PA, vagyis hogy ami kötelező, az megengedett - ami pedig, logikai értelemben, meglehetősen gyenge állítás (az ebből levezethető állítások körében jellemzően a triviálishoz közelítők találhatók). Másrészt, míg a klasszikus modális logikának logikai igazsága ("törvénye"), hogy A->◊A, addig szintén könnyen belátható, hogy a deontikus logikában nem igaz, hogy A->PA, vagyis az, hogy egy cselekmény végrehajtásából következne, hogy az meg van engedve.

[27] Több kísérlet is történt a deontikus logika alethikus logikára való visszavezetésére, redukciójára. Stig Kanger[37] egy megkülönböztetett propozícióval dolgozott: d szándékolt jelentése az, hogy minden normatív követelmény teljesítve van, minden szabály be van tartva ("all normative demands are met"). A kötelezőséget mint egy állítás (cselekmény) státuszát úgy fejezi ki, mint ami a kitüntetett propozícióból következik: Op =df □(d -> p), vagyis az, hogy valami kötelező, azt jelenti, hogy minden szabály betartásakor szükségszerűen (biztosan) teljesül. A megengedettséget pedig úgy, mint ami összefér minden szabály betartásával: Pp =df ◊(d & p). Valamennyi modalitás kifejezhető így, és bizonyítható, hogy Kanger erre épített logikája tartalmazza a sztenderd deontikus logikát (vagyis valamennyi olyan állítás, amely tétele a sztenderd deontikus logikának, tétele ennek a rendszernek is). A rendszerből ezenfelül levezethető néhány további - intuitív - tétel, például az, hogy d kötelező (Od) és hogy ami kötelező, az lehetséges: Op -> ◊p. Ez utóbbi tételre gyakran Kant törvényeként hivatkozunk a Tiszta ész kritikájában kifejtett elvárás miatt ("Sollen impliziert Können", bár Kant törvénye egy adott ágenshez kötötte a két modalitás közötti elvárt kapcsolatot).

[28] Kangerrel egy időben, tőle függetlenül dolgozott ki egy hasonlóan reduktív rendszert Alan Ross Anderson.[38] Anderson az s állítást vette definiálatlan, kitüntetett propozíciónak, azzal a szándékolt jelentéssel, hogy egy szankció esedékes ("sanction has been evoked", "there is a liability to sanction"). Ez az állítás definiálható d negációjaként is, azzal a jelentéssel, hogy némely szabály nincs betartva: s =df ~d. Ez az alternatív kiindulópont értelemszerűen valamelyest különböző axiómákat követel meg a rendszer felépítésekor. Míg Kangernek azt kellett feltételeznie, hogy lehetséges, hogy minden szabály be van tartva (◊d), addig Andersonnak az ezzel ekvivalens axiómát, hogy (logikailag) nem szükségszerű, hogy némely szabály nincs betartva (~□s). Anderson a kötelezőséget a következőképpen definiálta: Op =df □(~p -> s), vagyis szükségszerű, hogy ha p nem teljesül, akkor a szankció esedékessé válik.

[29] A deontikus modalitások alethikus modalitásokra való redukálhatósága erősítheti azt a nézetet, hogy adekvát az igaz-hamis distinkció mentén kezelnünk a normák logikáját, de fontos látni, hogy a redukció teljessége látszólagos: a kiindulópontként használt propozíciók valójában normatív tartalmat rejtenek. Az olyan kifejezések, mint a normative demand, a sanction vagy a liability nem sokban különböznek a "kötelező" deskriptív olvasatától, konceptuális elemzésükkel visszajutnánk a kötelezőség fogalmához,[39] ez redukció helyett valójában körkörösséghez vezetne. A látszólagos deskriptív jelleg kérdése összefügg a konstitutív normák elméletével is (lásd alább).

[30] A deontikus modalitások közül a megengedettség sokat vitatott fogalom. Az 1951-es von Wright-i rendszerben és az azzal csaknem azonos sztenderd deontikus logikában a megengedettség a kötelezettség duálisa: pontosan akkor megengedett egy cselekmény, ha a végre nem hajtása (tőle való tartózkodás) nem kötelező. Vagyis minden megengedett, ami nem tilos: azaz amit kifejezetten nem tilt meg a jogszabály, azt megengedi.[40] Sokat vitatott kérdés azonban, hogy ettől miben különbözik az, amikor a jogszabály kifejezetten megenged valamit. A deontikus logikai irodalom az elsőt gyenge, míg az utóbbit erős megengedésnek hívja (weak and strong permission). Míg a sztenderd deontikus logikának (karakterisztikus) axiómája az, hogy ha valami kötelező, akkor az megengedett (Op -> Pp) - hiszen ha ez nem lenne igaz, ellentmondás lenne a rendszerben -, ez az összefüggés bizonyosan nem áll az erős megengedésre: nagyon furcsa lenne, ha a jogszabály valamely kötelesség rögzítését követően az adott cselekményt kifejezetten meg is engedné. Így azon rendszerekben sem lehet ez axióma, amelyek a Pp igazságához kifejezett megengedést kötnek. A logikai rendszerek számára ellenben valóban feloldandó probléma, hogy jogelméleti szempontból van-e különbség azon cselekmények jogi megítélése között, amelyeket kifejezetten megenged a törvény, és amelyekről nem rendelkezik. Arend Soeteman amellett érvel, hogy míg deskriptív szempontból van különbség (létezik-e megengedő norma), preskriptív szempontból nincs - úgy tűnik, amellett foglal állást, hogy a joghatás szempontjából nincs különbség a két fajta megengedés között.[41]

[31] Hogyan alakul a deontikus modalitások beazonosíthatósága a jogban (elsősorban ->a kontinentális jogrendszerekről beszélve), a jogszabályokban? Míg az imperatív nyelvhasználatnak a felszólító mód a legkézenfekvőbb megjelenési formája, a jogban csak kijelentő mondatokat találunk,[42] a preskriptív jellegnek más nyomát kell keresni. A magyar joginyelv-használatban különböző módjai vannak a kötelezőség kifejezésének: a jogszabályszövegben egyértelműen kötelezésként azonosíthatók azok - az egyébként kijelentő - mondatok, amelyekben a "kötelező" (esetleg a "szükséges") szó vagy valamely beálló melléknévi igenév állítmányi szerepben van, és ahol deontikus segédige (például "kell") található a mondatban. Vannak azonban olyan mondatok, amelyekben nem szerepel egyik sem, ahogyan a megengedettség vagy a tilalom semmilyen nyelvi jele sem: ezek - látszólag - tisztán leíró jellegű mondatok. A magyar legisztikai irodalom szerint ezek a mondatok is normatívak: mind Tamás András, mind Tóth Judit úgy tartja, a kijelentő módú (leíró jellegű) mondatok is kötelezést takarnak a jogszabályban.[43]

[32] Ez összhangban áll azzal a közkeletű megkülönböztetéssel két normatípus között, amelyet (John Rawls[44] és) John Searle[45] elméleteiből ismerünk: a searle-i regulatív normák (Rawlsnál: summary rules) eleve - a normától függetlenül - létező cselekményeket szabályoznak, nyelvileg jellemzően preskriptív (akár imperatív) formában, míg a konstitutív normák (Rawlsnál: practice rules) által szabályozott cselekmények léte logikailag függ a konstitutív normától. Az utóbbi csoportba tartozó normák szintén lehetnek esetenként nyelvileg is preskriptívek, de jellemzően inkább tisztán leíró jellegük van, azonban mégis "szabálynak számítanak".[46] A konstitutív normák legjellemzőbb szerkezete az ún. "counts-as" szabály, azaz amikor a norma egy valós tényt jogi vagy intézményi (institutional) tényként azonosít. A counts-as normák jogelméleti és legisztikai jelentőségét érzékletesen mutatja be Alf Ross híres, Tû-tû (Bragyova András fordításában[47] Tyu-tyu) című cikke.[48] Az ilyen típusú normák formalizálása - még ha preskriptívek is valamilyen értelemben - soha nem a kötelezés operátor használatával, nem is deontikus logikával történik, hanem jellemzően valamilyen ún. feltételes logikával (conditional logic).[49]

[33] A tilalmak beazonosítását illetően is találhatók a magyar jogi nyelvben sajátosságok. A "tilos" állítmányi szerepben való szerepeltetésén túl a megengedettség tagadása is adekvát és könnyen beazonosítható nyelvi jele a tilalomnak. A Büntető Törvénykönyv (Btk.)[50] azonban különös tanulsággal szolgál a modalitások nyelvi megjelenése, egymás közötti összefüggése és jogelméleti szerepe tekintetében. Míg a Btk. különös része épp azokat a cselekményeket sorolja fel, amelyek deontikus minősítését illetően aligha van kétségünk a tilalom felől, a "tilos" szó vagy a fent említett nyelvi megoldások egyike sem szerepel a jogszabályban. Az egyetlen modalitás, amivel találkozunk, beálló melléknévi igenév formájában szerepel:

160. § (1) Aki mást megöl, bűntett miatt öt évtől tizenöt évig terjedő szabadságvesztéssel büntetendő.

Vagyis, amennyiben elfogadjuk, hogy a hatályos magyar jogszabályok, egész pontosan a Btk. szerint tilos az emberölés, azt találjuk, hogy a tilosságot (tilalmat) mint modalitást a büntetésre kötelezéssel fejezi ki.

[34] Von Wright a Norm and Action utolsó fejezetében foglalkozik a normák rendjével: megkülönböztet első- és magasabb rendű normákat (first- and higher-order norms). Az elsőrendű normák valamilyen - nem normatív -aktust szabályoznak, míg a magasabb rendű normák normatív, azaz normák megalkotására irányuló aktusokat. Bár von Wright nem állítja kifejezetten, a leírásból úgy tűnik, az első- és a magasabb rendű normák halmazait diszjunktnak tekinti. A Btk. 160. §-a (és csaknem valamennyi szakasz a különös részből) azonban egyszerre elsőrendű norma, hiszen megtiltja az emberölést, és magasabb rendű norma is, hiszen a büntetni rendelés a tilalom kifejezésének eszköze: norma a bíró számára a büntetés kiszabására. Vagyis a jogban a két halmaz nem diszjunkt: a Btk-beli normák azáltal elsőrendű normák, hogy magasabb rendű normák.[51]

[35] A kifejezett (erős) megengedés nyelvi jele lehet egyrészt a "megengedett" kifejezés, a deontikus (és nem alethikus) értelemben használt "lehet" és a hatóképzős igéből képzett folyamatos melléknévi igenév állítmányként való szerepeltetése, vagy egyszerűen a hatóképzős ige (szintén előfordul a kötelezés tagadása: "nem kell", "nem kötelező"). Fontos azonban, hogy nem valamennyi ilyen formájú mondat azonosítandó megengedésként: a hatóképzős ige mint állítmány sokszor valamilyen jogosultságot jelöl. A jogosultság - különböző formáinak - deontikus modalitáskora való visszavezetése pedig korántsem egyértelmű.

[36] A jogosultságok (rights) jogelméleti irodalma nagyon kiterjedt, itt csak a hohfeldi jogosultságelméletre térünk ki röviden ki, ez szolgáltatja ugyanis a deontikus logikában egy speciális fogalomnak, az ún. normatív pozícióknak az elméleti hátterét. Wesley Newcomb Hohfeld 1913-as esszéjében[52] abból a terminológiai és ezzel együtt konceptuális zavarból kiindulva, hogy a "jogosultság" (right) kifejezés túl- és pontatlanul használt még a jogászok körében is, elkülönít négy logikailag lehetséges jogosultságfajtát és az azokkal mindig (szükségszerűen, fogalmilag) együtt járó négy kötelezettségfajtát:

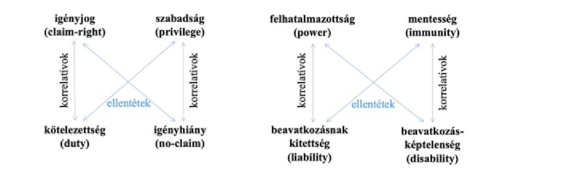
3. ábra

A hohfeldi jogosultságok, kötelezettségek és viszonyaik[53]

Az első négyzet normatív pozícióit statikus pozícióknak szokás hívni a jobb oldali négyzet dinamikus pozícióival szemben, ugyanis míg a bal oldali pozíciók hatókörében egyszerű cselekmények állnak, a jobb oldali pozíciók olyan cselekményekre vonatkoznak, amelyek alkalmasak más normatív pozíciók megváltoztatására.

[37] A hohfeldi elmélet leglényegesebb eleme a (deontikus) logika szempontjából az, hogy ágenssekkel, egészen pontosan ágenspárokkal dolgozik, vagyis állítása szerint a klasszikus személytelen deontikus modalitásokhoz ágenseket kell bevezetni a formális elméletbe. A szűkebb értelemben vett kötelezettség (duty) csak annyiban különbözik a sztenderd deontikus logikában használt kötelességfogalomtól, hogy irányított:[54] a hohfeldi rendszer lényege, hogy az egyik fél joga, ez esetben igényjoga (követelése) a másik fél kötelezettségét jelenti az előző fél irányában. Vagyis ha ezeket a modalitásokat be akarjuk vezetni a deontikus logikába, valójában csak relativizálnunk kell az O operátort egy ágenspárra (és a köztük levő irányra): Oxày. Mivel a korrelativitás logikai értelemben ekvivalenciát jelent, az igényjog jelöléséhez nem kell új modalitást (operátort) bevezetnünk: x irányított kötelezettsége y felé y igényjogát jelenti arra, hogy x az igényjog tárgyát jelentő cselekvést végrehajtsa. A hohfeldi szabadság a deontikus gyenge megengedéssel ekvivalens pozíció (kivéve, hogy ágenspárra relativizált): az adott kötelezettség hiányát jelenti (azaz egy negált formula), ahogyan az ezzel korrelatív igényhiány is (ahogyan azt a neve is mutatja). Más a helyzet azonban a dinamikus pozíciókkal: ezek logikai kezelése másfajta logikát igényel: a legújabb formalizálások[55] mind ún. dinamikus logikákat használnak. Szemben a klasszikus logikával, ahol a mondatok jelentését igazságfeltételekkel jellemezzük, a dinamikus logikában valamilyen állapotváltozással: jelen esetben a normatív pozíciók megváltozásával.

[38] Márpedig a hohfeldi felhatalmazottságot különösen fontos adekvát módon elkülöníteni a megengedettségtől: nyelvi megjelenésükben jellemzően nagyon hasonlóak lehetnek (például hatóképzős igék), ám a - logikai és jogi - következményük meglehetősen különböző. David Makinson hívja fel erre a fontos különbségre a figyelmet: ha valaki egy cselekményt megengedés hiányában végrehajt, az valamilyen szankciót fog kiváltani, míg ha valaki felhatalmazottság hiányában próbál meg egy cselekményt végrehajtani, a cselekménye nem fog megvalósulni.[56] Azon igék hatóképzős alakjai, amelyek konstitutív normák által létrehozott, jogi cselekményt takarnak, általában felhatalmazottságként értelmezendők, míg általános, a jogtól függetlenül létező, egyszerű cselekményeket leíró igék hatóképzős formái bizonyosan megengedést, hiszen ez utóbbi cselekmények nem változtatnak normatív pozíciókat, így nem lehetnek felhatalmazottság hatókörében.[57]

4. Logikai és jogi érvényesség, a logika alkalmazásának értelme és szükségessége a jog elemzésében

[39] Ha elfogadjuk, hogy a logikának annak ellenére vannak adekvát eszközei a jog, a jogi fogalmak és a jogi normák elemzéséhez, hogy a normák nem bírnak igazságértékkel, kérdés maradhat, hogy miért használnánk őket. Solt Kornél ezt szemléletesen úgy fogalmazta meg: "[E]mpirikus tény, hogy vannak inkonzisztens érvényes normatív kódexek. A normák és kódexeik érvényessége elvileg érzéketlen a logikával szemben."[58] Valóban, ha a jogi érvényességet ahhoz a feltételhez kötjük, hogy a jogszabály (tervezete) egy meghatározott eljárás keretében a meghatározott testület által, annak felhatalmazásánál fogva jött létre (->jogalkotás), a logikának nem sok szerep marad. Szabó Miklós így ír erről:

Politikailag annak a politikai úton kialakított testületnek (a parlamentnek) a legitimitásától függ, amely fel van hatalmazva jogalkotásra; jogilag pedig annak az eljárásnak a betartásától, melyet más jogszabályok a jogalkotásra előírnak: az arra felhatalmazott szerv az előírt eljárás során hozza meg és hirdesse ki.[59]

[40] Viszont beszélhetünk tartalmi érvényességről is: "a megalkotott jogszabály nem ellenkezik magasabb szintű, a jogforrási hierarchiában előrébb helyet foglaló jogszabály előírásainak tartalmával".[60] Az "ellenkezés" minden valószínűség szerint ellentmondást, inkonzisztenciát jelent, ami pedig logikai kérdés, így bizonyos vonatkozásban van szerepe még a jogi érvényesség kérdésében is annak, hogy konzisztens-e egy jogrendszer. A jogszabályszerkesztésről szóló IRM rendelet első érdemi rendelkezése a következő:

2. § A jogszabály tervezetét a magyar nyelv szabályainak megfelelően, világosan, közérthetően és ellentmondásmentesen kell megszövegezni.

Az ellentmondásmentesség logikai fogalom, viszont a rendelkezés a megszövegezés tekintetében köti azt ki, így nem világos, mennyire érinti a jogszabályok tartalmát. Így bár a magasabb rendű jogszabályok viszonylatában van tartalmi elvárás az ellentmondásmentességet illetően, a hierarchiában azonos szinten elhelyezkedő jogszabályok egymás közötti esetleges ellentmondásának kiküszöbölését illetően nem találunk kifejezett (saját magával szemben támasztott) jogalkotói elvárást.

[41] Az ellentmondásmentesség elvárásának jogfilozófiai megalapozása azonban nem tűnik nehéznek: egymásnak ellentmondó szabályokat nem lehet (egyszerre) betartani, azaz amennyiben a jogalkotás céljának a személyi hatály alá eső jogalanyok viselkedésének meghatározott irányú befolyásolását tekintjük, ez magával hozza az ellentmondásmentességet, legalábbis az arra való törekvést mint elvárást. Von Wright a pályája végén a jogalkotásra mint racionalitás által vezérelt cselekményre gondolt, és a racionalitás épp ezt az ellentmondásmentességet támasztja elvárásként a jogalkotóval szemben. Ez a megközelítés tulajdonképpen normatív olvasatot ad magának a deontikus logikának: egy konzisztens deontikus logika nem leírja, hogyan működik a jog vagy bármilyen normatív rendszer, hanem hogy hogyan kell(ene) működnie.

[42] A jogi normák, jogi fogalmak adekvát formális (szimbolikus) reprezentációja az esetek jelentős részében előfeltétele a mesterséges intelligencia alkalmazásának. Az utóbbi időben egyre nagyobb teret nyerő gépi tanulásos és neurális hálóra épülő megoldások (sub-symbolic AI) kapcsán is egyre nagyobbnak tűnik a szakmai konszenzus azt illetően, hogy hosszú távon, a demokratikus és alkotmányos elvárásoknak való megfelelést csak formális módszerek (symbolic AI) ötvözésével lehet biztosítani.[61] Ennek nem csak a jogi eljárásokban alkalmazott megoldások, jogi informatikai alkalmazások kapcsán van jelentősége. A - nem tudjuk mennyire - távoli jövőben majdan kifejlesztett (autonóm[62]) mesterséges ágensektől[63] is szabálykövető magatartást várunk el, képesnek kell lennünk a betartandó szabályok gép által olvasható reprezentálására és megfelelő implementálására. Az AI&Law computer science alá eső területeinek és az ún. komputációs jognak a bemutatása és vizsgálata (több) külön szócikket igényelne, annyit azonban szükséges itt is rögzíteni, hogy a jog logikai vizsgálata nem (csupán) filozófiai eszmefuttatás többé, hanem nagyon is gyakorlati jelentőségű kérdés és rendkívül aktív kutatási terület. Ez persze nem jelenti azt, hogy a jogelméleti és filozófiai vizsgálódás mellőzendő lenne, épp ellenkezőleg: ezek folyamatos kutatására, tárgyalására van szükség a fejlesztendő logikai modellek adekvát megalapozásához. Ezek a modellek ugyanis egyre nagyobb szerepet kapnak a különböző AI&Law alkalmazásokban, és mind szakmabeliként, mind állampolgárként azzal az elvárással ildomos ezekhez közelítenünk, hogy magával a joggal, illetve egyes alrendszereivel megfelelő korrespondenciát mutassanak.■

5. JEGYZETEK

[1] Jørgen JØRGENSEN: "Imperatives and Logic" Erkenntnis 1937/1, 288-296.

[2] Az alanyi vonatkozói mellékmondat jelentőségéről a jog(alkotó)i nyelvben lásd SAJGÁL Mónika: "Alárendelés a magyar jogi nyelvben" in SZABÓ Miklós - VINNAI Edina (szerk.): A törvény szavai, Prudentia Iuris 33, Miskolc, Bíbor, 2018, 123-151.

[3] SOLT Kornél: Jog és Logika, Budapest, Seneca, 1996.

[4] Ota WEINBERGER: Philosophische Studien zur Logik II (Phiosophische Bemerkungen zur Sollsatzlogik), Praha, Rozpravy Československé Akadémie věd, 1964, 5 alapján SOLT (3. j.) 289.

[5] Georg H. VON WRIGHT: "Deontic Logic" Mind 1951/237, 1-15. A címet, amivel egy egész diszciplínát nevezett el, von Wright egy lábjegyeztben tanárának, C. D. Broadnak köszöni meg. Valójában Ernst Mally, Meinong tanítványa volt az első, aki ezt a szót használta, "deontik" formában, és bár a deontikus logika első szisztematikus rendszerének (pontosabban: szintaxisának) kidolgozását egyértelműen von Wrighthoz kötjük, Mally 1926-ban megjelent monográfiájában (Grundgesetze des Sollens: Elemente der Logik des Willens) felállított egy axiomatikus rendszert, ami azonban súlyosan kontraintuitív tételekhez vezetett (például Op akkor és csak akkor igaz, ha p, ami ugye azt jelentené, hogy minden, ami történik az kötelező, és ami kötelező, az meg is valósul). Mally rendszerének angol nyelvű összefoglalását lásd például Dagfinn FOLLESDAL - Risto HILPINEN: "Deontic Logic: An Introduction" in Risto HILPINEN (szerk.): Deontic Logic: Introductory and Systematic Readings, Dordrecht, Reidel, 1971, 1-35, illetve Gert-Jan LOKHORST: "Mally's Deontic Logic" in Edward N. ZALTA (szerk.): The Stanford Encyclopedia of Philosophy (Summer 2019 Edition).

[6] Standard Deontic Logicként - SDL-ként - a logikusok az ún. KD modális kalkulusra - és a hozzá tartozó Kripke-szemantikára - szoktak hivatkozni. Ugyancsak szokás ezt a logikát Monadic Deontic Logicnak nevezni, megkülönböztetendő egy későbbi, sokak szemében szintén sztenderddé váló logikától, ahol diadikus modális operátort (és preferenciaalapú szemantikát) használunk. Míg a modális kalkulusok és a Kripke-szemantika mibenlétére minimális laikus bevezetést a jelen szócikk későbbi részei tartalmaznak, a diadikus deontikus logikára nem térünk ki. Történeti részletekért és technikai bevezetőért lásd Risto HILPINEN - Paul MCNAMARA: "Deontic Logic: A Historical Survey and Introduction" in Dov GABBAY -- John HORTY - Xavier PARENT - Ron VAN DER MEYDEN - Leendert VAN DER TORRE (szerk.): Handbook of Deontic Logic and Normative Systems, London, College Publications, 2013, 3-136.

[7] Nagyon fontos az ezek közötti összefüggés: ha a levezetési szabályokkal levezethető formulák mind igazak a szemantika szerint, akkor az adott logika helyes (sound); ha minden olyan formula, ami igaz a szemantika szerint, levezethető, akkor az adott logika teljes (complete). A helyes és teljes logikákat magyarul adekvátnak nevezzük.

[8] A lehetséges világok elméletén alapuló formális szemantika kidolgozását a modális logika számára Saul Kripke nevéhez szokás kötni. A lehetségesvilág-szemantika a matematikában járatlanok számára viszonylag bonyolult konstrukció, így ennek az ismertetésére itt nem térünk ki; a matematikában jártas olvasó számára pedig annyi elég lehet, hogy olyan modellekről van szó, amelyekben a kötelezőség egy univerziális, a megengedettség pedig egy egzisztenciális kvantifikáció egy bináris elérhetőségi reláció mentén, amellyel szemben az egyetlen elvárás a deontikus jelleg karakterizálásához az, hogy szeriális legyen (kizárva a dead end világokat, vagyis biztosítva, hogy ne lehessen p és ~p egyszerre kötelező).

[9] Georg VON WRIGHT: Norm and Action, London, Routledge and Kegan Paul, 1963.

[10] Kelsen normalogikát érintő álláspontjának elemzését lásd SZABÓ Miklós: "Hans Kelsen esete a normalogikával" Világosság 2005/10, 73-82.

[11] "Az évek során a nézetem egyre »radikálisabbá« vált, és kezdtem azt gondolni, hogy az olyan logikai viszonyok, mint az ellentmondás és következmény nem tarthatók a (valódi) normák esetén, s ezért bizonyos értelemben nem lehetséges olyasmi, mint a »normalogika«". Georg VON WRIGHT: "Is there a logic of norms?" Ratio Juris 1991/3, 265-283; magyar fordítása: BÓDIG Mátyás - SZABÓ Miklós (szerk.): Logikai olvasókönyv joghallgatók számára, 2. javított kiadás, Prudentia Iuris 4, Miskolc, Bíbor, 1996, 133.

[12] David MAKINSON: "On a Fundamental Problem of Deontic Logic" in Paul MCNAMARA - Henry PRAKKEN (szerk.): Norms, Logics and Information Systems. New Studies in Deontic Logic and Computer Science, Frontiers in Artificial Intelligence and Applications 49, Amsterdam, IOS Press, 1999, 29-53.

[13] Erik STENIUS: "Principles of a logic of normative systems" Acta Philosophica Fennica 1963/16, 247-260.

[14] Carlos ALCHUORRÓN - Eugenio BULYGIN: "The expressive conception of norms" in Risto HILPINEN (szerk.) New Essays in Deontic Logic, Dordrecht, Reidel, 1981, 95-124, valamint Carlos ALCHUORRÓN: "Philosophical foundations of deontic logic and the logic of defeasible conditionals" in J.J. MAYER - R.J. WIERINGA (szerk): Deontic Logic in Computer Science, New York, Wiley, 1993, 43-84.

[15] Fontos megjegyezni, hogy elméletben az indukció ugyanúgy járhat teljes bizonyossággal: ha valamely kategória összes elemét számba tudjuk venni (ami a jogban ritkán fordul elő), akkor magáról a kategóriáról is alkothatunk bizonyossággal ítéletet. Magában a matematikában is az egyik legáltalánosabb bizonyítási módszer az induktív bizonyítás, amit induktív definícióval bevezetett adott osztály elemeire lehet használni (például a természetes számok aritmetikájában gyakran használt teljes indukció).

[16] Henry PRAKKEN: Logical Tools for Modelling Legal Argument, Amsterdam, Vrije Universiteit, 1993, 15.

[17] Prakken ebben a körben tárgyalja Philip Leith cikkét és Stephen Toulmin könyvét, lásd Philip LEITH: "Fundamental Errors in Legal Logic Programming" The Computer Journal 1986/6 545-552; Stephen TOULMIN: The Uses of Argument. Cambridge, Cambridge University Press, 1958. Idesorolható továbbá Chaïm PERELMAN: Logique juridique. Nouvelle rhétorique, Paris, Dalloz, 1976, magyarul bemutatja SZABÓ Miklós: Logica Magna, Miskolc, Bíbor, 2014, 163-166.

[18] SZABÓ (17. j.) 141.

[19] "»Az érvényes szerződés meglétének vannak szükséges pozitív feltételei« de vannak tényezők, amelyek ezt az érvényességet alááshatják »akkor is, ha minden szükséges feltétel teljesült«" H. L. A. HART: "The ascription of responsibility and rights" in Anthony FLEW (szerk.): Logic and Language, Oxford, Blackwell, 1951 alapján Davide GROSSI - Antonino ROTOLO: "Logic in the Law. A Concise Overview" 2011, 8, (a szerző fordítása).

[20] A jogban több szinten is szokás defizibilitást detektálni, részletesen lásd GROSSI-ROTOLO (19. j.) 8-12; Henry PRAKKEN - Giovanni SARTOR: "The three faces of defeasibility in the law" Ratio Juris 2004/1, 118-139.

[21] SZABÓ (17. j.) 141.

[22] Lásd Donald NUTE (szerk.): Defeasible Deontic Logic, Synthese Library (Studies in Epistemology, Logic, Methodology, and Philosophy of Science) 263, Dordrecht, Springer, 1997.

[23] Ebbe a diszciplínába bevezetésül szolgálhat Pietro BARONI - Dov GABBAY - Massimiliano GIACOMIN - Leendert VAN DER TORRE (szerk.): Handbook of Formal Argumentation, College Publications, 2018.

[24] A jogalkalmazó (igazságszolgáltatás) egy adott eset tényeire alkalmazva a jogot értelmezi azt; ha egy mérnök teszi ezt meg előzetesen, az elhamarkodott (premature). LEITH (17. j.) 546.

[25] A "csak akkor..., ha..." forma egyértelműen retrokondicionálist jelöl. Az "akkor..., ha..." felépítésű megnyilatkozások azonban többféle hangsúllyal is megtehetők, így írásban nem világos, hogy a felcserélt sorrend jelenti-e, hogy a beszélő szükséges, és nem elégséges feltételre utal.

[26] Ezek az igazságfüggvények szemantikai szempontból igazságtáblákkal ábrázolhatók. A kondicionális, a retrokondicionális és a bikondicionális igazságtáblája:

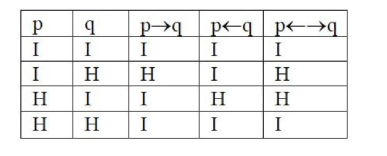
[27] Az egyes feltételes mondatok nyelvtani szerkezetnek elemzéséről lásd MARKOVICH Réka - HAMP Gábor - SYI: "A kondicionálisok problémája jogszabályszövegekben" in TANÁCS Attila - VARGA Viktor - VINCZE Veronika (szerk.): X. Magyar Számítógépes Nyelvészeti Konferencia konferenciakötete, Szeged, Szegedi Tudományegyetem, 2014, 295-302.

[28] Trevor BENCH-CAPON - Marek SERGOT: "Towards a Rule-based Representation of Open Texture in Law" in Charles WALTER (szerk.): Computing power and legal language, Westport, Greenwood-Quorum, 1988, 39-60.

[29] Layman E. ALLEN - Charles S. SAXON: "More IA needed in AI: Interpretation Assistance for Coping with the Problem of Multiple Structural Interpretations" in Proceedings of the Third International Conference on Artificial Intelligence and Law, ICAIL '91, Oxford, England, June 25-28, New York, ACM , 1991, 53-61.

[30] A jogszabályszerkesztésről szóló 61/2009. (XII. 14.) IRM rendelet.

[31] "4. § (1) Ha egy jogszabályon és a végrehajtására kiadott jogszabályokon belül ugyanazt a fogalmat vagy rendelkezést többféleképpen is ki lehet fejezni, a fogalom vagy rendelkezés valamennyi előfordulása esetében ugyanazt a megfogalmazást kell alkalmazni.

(2) Egy jogszabályban és a végrehajtására kiadott jogszabályokban azonos szabályozási tárgyra vonatkozó különböző megfogalmazások csak akkor alkalmazhatóak, ha azok eltérő tartalmat fejeznek ki."

[32] A különböző modális értelmezések mentén létrejövő logikai rendszerek párhuzamosságát szemléletesen mutatja be Georg H. VON WRIGHT: An Essay in Modal Logic, Amsterdam, North-Holland, 1951.

[33] A ~, &, v, ->, ↔ jelek a negáció, konjunkció, diszjunkció, kondicionális és bikondicionális konnektívumokat jelölik (ebben a sorrendben). (Más jelölési hagyományban az első hármat gyakran a Ø, Ù és Ú jelekkel jelölik).

[34] Matthias Armgardtnak számos munkája foglalkozik részletesen Leibniz ilyen irányú munkásságával, például Matthias ARMGARDT: "Presumptions and Conjectures in the Legal Theory of Leibniz" in Mathias ARMGARDT - Patrice CANIVEZ - Sandrine CHASSAGNARD-PINET (szerk.): Legal Reasoning and Logic - Past and Present Interactions, Cham, Springer, 2015, 51-69.

[35] Berislav ŽARNIĆ - Gabriela BAŠIĆ: "Metanormative Principles and Norm Governed Social Interaction" Revus 2014/22, 105-120.

[36] Az intuitív kiolvasás érdekében a deontikus hatszögben cselekmények (végrehajtásának) deontikus státuszát jelöltük, de ahogyan azt már fentebb jeleztük, A cselekmény helyén állhat egy tetszőleges p állítás (csakúgy, mint az alethikus hatszögben), ez nem befolyásolja a modalitások egymás közötti viszonyát.

[37] Stig KANGER: "New Foundations for Ethical Theory" in Risto HILPINEN: Deontic Logic: Introductory and Systematic Readings, Dordrecht, Springer, 1971, 36-58.

[38] Alan Ross ANDERSON: The Formal Analysis of Normative Systems, New Haven, Yale Sociology Department, 1956, 147-213 és "A Reduction of Deontic Logic to Alethic Modal Logic" Mind, 1958/265, 100-103.

[39] A normatív követelmény tulajdonképpen ugyanazt jelenti, hogy a "kötelező", a szankció egy kötelező cselekmény végre nem hajtása miatti jogkövetkezmény (vagyis az, amit mint következményt a jog kötelezővé tesz), míg a jogi felelősség (liability) is egy kötelezettséggel kapcsolatban közvetlenül fellépő fogalom - szankciónak kitettség.

[40] Von Wright a Deontic Logicban ezt még magától értetődőnek kezeli, a Norm and Actionben viszont már hosszasan elemzi, hogy helyes-e. Ami von Wright szerint ellene szól, az az, hogy a lehetséges cselekmények száma változik. Ameddig például nem tudták, hogyan kell desztillálni, nem voltak az alkoholfogyasztásra vonatkozó szabályok; ahol nincs házasság mint intézmény, ott nincs házasságtörés sem. Így kétfelé oszthatjuk a cselekményeket: amelyek léteznek és amelyek (még) nem. A létezőket és újonnan létrejövőket illetően a jogalkotó dönthet arról, kíván-e hozzájuk rendelkezést kapcsolni. Mindig lesznek, amikhez nem - ezek gyakorlása esetén aligha beszélhetünk törvénysértésről, így ebben az értelemben igenis megengedettek. Ekkor azonban el kell különítenünk a kétféle megengedést.

[41] Arend SOETEMAN: "The Negation of Normative Expressions: Weak and Strong Permission, Particularly in Law" in Arend SOETEMAN: Logic in Law, Dordrecht, Kluwer Academic Publications, 1989, 132-182.

[42] A jogszabályszerkesztésről szóló IRM rendelet ezt ki is köti: 3. § (2) "A jogszabály tervezetében a normatív tartalmat jelen idejű kijelentő mondattal, egyes szám harmadik személyű megfogalmazás alkalmazásával kell kifejezni."

[43] TAMÁS András: Legistica, Budapest, Szent István Társulat, 2009, 155; TÓTH Judit: Jogalkotástan. Egyetemi jegyzet, Budapest, Corvinus Egyetem, 2011, 50.

[44] John RAWLS: "Two concepts of rules" The Philosophical Review 1955/1, 3-32.

[45] John R. SEARLE: The construction of social reality, London, Penguin, 1996.

[46] Magyar jogi példákat és részletes kifejtését lásd MARKOVICH Réka: "A jogszabályok logikai mélystruktúrája" in SZABÓ-VINNAI (2. j.) 181-198 és MARKOVICH Réka: "Tilalom és kötelesség a számítógép szemével" in SZABÓ Miklós (szerk.): A jog nyelvi dimenziója, Miskolc, Bíbor, 2015, 267-274.

[47] SZABÓ Miklós - VARGA Csaba (szerk.): Jog és nyelv, Budapest, 2000, 121-131.

[48] Alf ROSS: "Tû-tû" Harvard Law Review 1957(70)/5, 812-825.

[49] Részletes összehasonlító elemzés a count-as normák formális reprezentációjáról lásd Davide GROSSI - Andrew J.I. JONES: "Constitutive norms and count-as conditionals" in GABBAY et al. (6. j.) 407-441.

[50] A Büntető Törvénykönyvről szóló 2012. évi C. törvény.

[51] Részeletes kifejtésért lásd MARKOVICH Réka: "Order of Norms and Deontic Modality" in South American Journal of Logic 2015/2, 435-445.

[52] Wesley Newcomb HOHFELD: "Az alapvető jogi fogalmak a bírói érvelésben" (ford. SZABÓ Miklós) in SZABÓ-VARGA (47. j.) 59-96.

[53] MARKOVICH Réka: "Nem házasságközvetítés, bikondicionálisok. Formulák, az állam és az emberi jogok" in HEGYI Szabolcs - VINNAI Edina - ZŐDI Zsolt (szerk.): Orbis Iuris. Tanulmányok Szabó Miklós 65. születésnapjára, Miskolc, Bíbor, 2016, 109-117.

[54] Az irányítottság jelentőségéről és a normatív pozíciók formalizálásának kihívásairól lásd David MAKINSON: "On the Formal Representation of Rights Relations: Remarks on the Work of Stig Kanger and Lars Lindahl" Journal of Philosophical Logic 1986/4, 403-425. A Hohfeld-esszé utáni első évszázad formalizálási kísérleteiről lásd Marek SERGOT: "Normative Positions" in GABBAY et al. (6. j.) 353-406.

[55] Lásd MARKOVICH Réka: "Understanding Hohfeld and Formalizing Legal Rights: the Hohfeldian Conceptions and Their Conditional Consequences" Studia Logica 2020/1, 129-158 és az abban hivatkozottak.

[56] MAKINSON (54. j.) 403-425.

[57] Részletes kifejtését lásd MARKOVICH (55. j.).

[58] SOLT (3. j.) 308.

[59] SZABÓ Miklós: "A jogforrás" in SZABÓ Miklós (szerk.): Bevezetés a jog- és államtudományokba, Miskolc, Bíbor, 1998, 27-52, 35.

[60] SZABADFALVI József: "A jogszabály" in SZABÓ (59. j.) 53-74, 69.

[61] Az egyik leggyakrabban emlegetett ilyen elvárás a transzparencia, magyarázhatóság: még ha vitatott is, hogy a GDPR rögzít-e magyarázathoz való jogot az automatikus (algoritmikus) döntés kapcsán az érintett számára, a magyarázható mesterséges intelligencia (explainable AI, XAI) az egyik legaktívabb kutatási terült a mesterséges intelligencián belül. (A right to explanation létezéséről lásd például Sandra WACHTER - Brent MITTELSTADT - Luciano FLORIDI: "Why a Right to Explanation of Automated Decision-Making Does Not Exist in the General Data Protection Regulation" International Data Privacy Law, 2017/2, 76-99.)

[62] Az autonómia technológiai fogalma folyamatos, intenzív diszkusszió tárgya, csak úgy, mint a pszichológiai és jogi autonómiafogalmakkal való kapcsolata.

[63] Az "ágens" szó itt a computer science-ben használt értelemben szerepel, a jogi ágenciafogalom egyelőre nincs ezekre kiterjesztve.